 por Danilo » Ter Nov 06, 2012 14:58
por Danilo » Ter Nov 06, 2012 14:58
Ache uma reta que passa pelo ponto (1,-2,3) e que forma ângulos de 45 graus e 60 graus com os eixos x e y respectivamente.
Sei que para eu encontrar a equação da reta falta apenas um vetor diretor desta reta. Mas eu não sei como usar a informação dos angulos formados com o eixo x e y e muito menos visualizar isso para resolver... grato a quem puder ajudar !
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Ter Nov 06, 2012 15:31
por MarceloFantini » Ter Nov 06, 2012 15:31
Seja
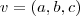
este vetor diretor unitário.
Se ele faz um ângulo de 45° com o eixo x, então o produto interno será
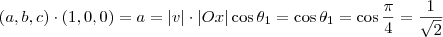
.
Analogamente, se ele faz um ângulo de 60° com o eixo y, então o produto interno será

.
Como

é unitário, então

e daí
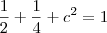
e

. Isto significa que existem dois vetores diretores que satisfazem:
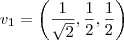
e

.
Portanto, uma destas duas retas satisfará o que o enunciado pede:
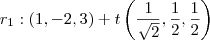
ou

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Danilo » Ter Nov 06, 2012 15:57
por Danilo » Ter Nov 06, 2012 15:57
MarceloFantini escreveu:Seja
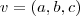
este vetor diretor unitário.
Se ele faz um ângulo de 45° com o eixo x, então o produto interno será
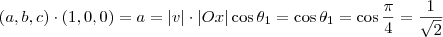
.
Analogamente, se ele faz um ângulo de 60° com o eixo y, então o produto interno será

.
Como

é unitário, então

e daí
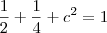
e

. Isto significa que existem dois vetores diretores que satisfazem:
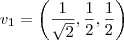
e

.
Portanto, uma destas duas retas satisfará o que o enunciado pede:
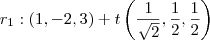
ou

.
Marcelo, por que você considerou o vetor v como sendo um vetor unitário? E por que o produto interno a (0,1,0) ? Grato!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Ter Nov 06, 2012 16:02
por MarceloFantini » Ter Nov 06, 2012 16:02
Unitário foi para facilitar, porque realmente não faz diferença. Se ele tivesse um outro módulo, sempre podemos colocá-lo unitário pois basta dividir pelo módulo. Então é mais fácil assumir unitário de cara. O produto interno com
é para encontrar a projeção no eixo y, assim como fiz no eixo x.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Danilo » Ter Nov 06, 2012 19:53
por Danilo » Ter Nov 06, 2012 19:53
MarceloFantini escreveu:Unitário foi para facilitar, porque realmente não faz diferença. Se ele tivesse um outro módulo, sempre podemos colocá-lo unitário pois basta dividir pelo módulo. Então é mais fácil assumir unitário de cara. O produto interno com
é para encontrar a projeção no eixo y, assim como fiz no eixo x.
Entendi!!!

-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Danilo » Ter Nov 06, 2012 20:09
por Danilo » Ter Nov 06, 2012 20:09
Valeu.. eu mesmo sanei minha dúvida

Editado pela última vez por
Danilo em Ter Nov 06, 2012 20:22, em um total de 3 vezes.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação vetorial da reta/plano
por Danilo » Dom Nov 04, 2012 13:23
- 2 Respostas
- 4884 Exibições
- Última mensagem por Danilo

Dom Nov 04, 2012 16:51
Geometria Analítica
-
- [Equação da Reta] Reta que passa por pontos do plano.
por acorreia » Qua Mai 02, 2012 17:31
- 1 Respostas
- 2463 Exibições
- Última mensagem por Russman

Qua Mai 02, 2012 21:25
Geometria Analítica
-
- AJUDA EQUAÇÃO VETORIAL/PARAMÉTRICA NO PLANO
 por Raquel Botura » Sex Nov 09, 2018 11:19
por Raquel Botura » Sex Nov 09, 2018 11:19
- 1 Respostas
- 8381 Exibições
- Última mensagem por Gebe

Sex Nov 09, 2018 17:13
Geometria Analítica
-
- Equação vetorial da reta
por Danilo » Qua Out 31, 2012 02:36
- 3 Respostas
- 2324 Exibições
- Última mensagem por MarceloFantini

Sex Nov 02, 2012 08:23
Geometria Analítica
-
- Encontrar equação (vetorial) da reta
por elisafrombrazil » Qua Abr 19, 2017 21:52
- 0 Respostas
- 1820 Exibições
- Última mensagem por elisafrombrazil

Qua Abr 19, 2017 21:52
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


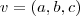 este vetor diretor unitário.
este vetor diretor unitário. 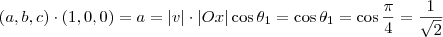 .
. .
. é unitário, então
é unitário, então  e daí
e daí 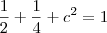 e
e  . Isto significa que existem dois vetores diretores que satisfazem:
. Isto significa que existem dois vetores diretores que satisfazem: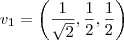 e
e  .
.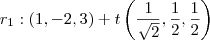 ou
ou  .
.

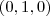 é para encontrar a projeção no eixo y, assim como fiz no eixo x.
é para encontrar a projeção no eixo y, assim como fiz no eixo x.





