 por fabriel » Sex Nov 02, 2012 13:57
por fabriel » Sex Nov 02, 2012 13:57
E ai pessoal, Resolvi essa integral mas estou com duvida no resultado, se é isso mesmo...Ve se eu errei nas contas ai...então é dada essa Integral:

Posso escreve-la assim, para decompor as frações:
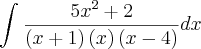
Então decompondo as frações, vamos ter o seguinte:

Isso vai nos levar ao seguinte:

Aí teremos o Sistema:

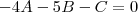

Logo:

e
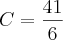
Teremos então:

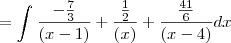
Calculando essa integral Vamos obter:
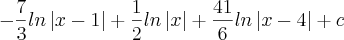
MAS AGORA EU POSSO SIMPLIFICAR ESSE RESULTADO?? SE SIM ENTÃO COMO QUE VAI FICAR??
(Um ótimo feriado a todos!!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por fraol » Seg Nov 19, 2012 22:00
por fraol » Seg Nov 19, 2012 22:00
Olá, boa noite.
A resolução está certa.
Há um lapso de digitação do sinal na 1a. fatoração do denominador mas está ok logo abaixo.
Quanto à simplificar, não há muito o que se possa fazer a não ser talvez usar o MMC de 3, 2 e 6 e colocá-lo em evidência na expressão final.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida Integral Indefinida
por cardoed001 » Sáb Fev 22, 2014 16:55
- 5 Respostas
- 4349 Exibições
- Última mensagem por Man Utd

Dom Fev 23, 2014 11:51
Cálculo: Limites, Derivadas e Integrais
-
- [integral indefinida] - dúvida
 por natanaelskt » Sáb Jun 28, 2014 09:25
por natanaelskt » Sáb Jun 28, 2014 09:25
- 3 Respostas
- 2605 Exibições
- Última mensagem por e8group

Sáb Jun 28, 2014 17:16
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL INDEFINIDA] Duvida de integração
por fabriel » Qua Out 03, 2012 16:20
- 3 Respostas
- 2078 Exibições
- Última mensagem por fabriel

Qua Out 03, 2012 17:39
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
por gdarius » Ter Mar 16, 2010 15:57
- 5 Respostas
- 5608 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 31, 2012 19:32
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
 por CrazzyVi » Ter Ago 17, 2010 21:41
por CrazzyVi » Ter Ago 17, 2010 21:41
- 1 Respostas
- 2701 Exibições
- Última mensagem por Lucio Carvalho

Qua Ago 18, 2010 08:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

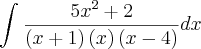



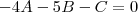

 e
e 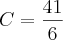

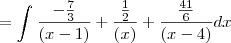
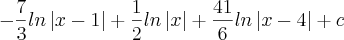



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
