Sub-seção para materiais das disciplinas relacionadas ao Instituto de Física.
Utilize a área de pedidos para outros ou caso a sub-seção da disciplina ainda não possua material.
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos, bibliografias etc.
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por Cleyson007 » Qui Nov 01, 2012 19:14
por Cleyson007 » Qui Nov 01, 2012 19:14
Seja o gráfico abaixo a velocidade da motocicleta de um policial em função do tempo.

a) Qual a aceleração instantânea para t = 3,0s, t = 7,0s e t = 11,0s?
b) Nos 5,0s iniciais qual o deslocamento do policial? E nos 9,0s inciais? E nos 13,0s iniciais?
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por young_jedi » Qui Nov 01, 2012 20:04
por young_jedi » Qui Nov 01, 2012 20:04
entre 0 e 5s a velocidade é constante portanto não a variação da mesmo sendo asssim a aceleração é igual a 0
de 5s a 9s podemos ver que a velocidade aumenta segundo uma reta, como a aceleração é a derivada da velocidade, a aceleração é dada pela inclinação desta reta portanto podemos calcular como

nos instantes de 9 a 13s a velocidade decai de acordo com outra reta, portanto a aceleração é a inclinação da mesmo ou seja
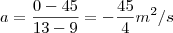
a) o deslocamento é igual a integral da velocidade, mais nos sabemos que a integral é igual a area abaixo da curva, portanto calculando esta area nos teremos o deslocamento
ate 5s temos a area de um quadrado
d(5)=20.5=100m
para os nove iniciais nos temos que calcular a area do quadrado ate 5s e do trapezio de 5s ate 9s

e nos 13s calculamos a area do quadrado 0 ate 5s, do trapezio de 5s ate 9s e do triangulo de 9s ate 13s
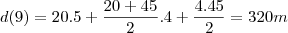
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Física
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cinemática] Inversão de movimento + grafico
por XxXMarlonXxX » Dom Out 07, 2012 02:16
- 3 Respostas
- 4452 Exibições
- Última mensagem por XxXMarlonXxX

Dom Out 07, 2012 15:53
Dúvidas Pendentes (aguardando novos colaboradores)
-
- Movimento de uma partícula
por Cleyson007 » Sex Jul 27, 2012 16:17
- 1 Respostas
- 1544 Exibições
- Última mensagem por MarceloFantini

Sex Jul 27, 2012 16:56
Física
-
- Felino em movimento
por Cleyson007 » Qui Nov 01, 2012 18:58
- 2 Respostas
- 1867 Exibições
- Última mensagem por e8group

Qui Nov 01, 2012 20:02
Física
-
- Mala em movimento
 por Cleyson007 » Ter Jan 15, 2013 16:41
por Cleyson007 » Ter Jan 15, 2013 16:41
- 5 Respostas
- 6224 Exibições
- Última mensagem por Cleyson007

Qui Jan 17, 2013 09:02
Física
-
- Carro em movimento
por Cleyson007 » Qua Fev 27, 2013 11:59
- 1 Respostas
- 2443 Exibições
- Última mensagem por young_jedi

Sex Mar 01, 2013 22:29
Física
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.








 .
.



