 por TheKyabu » Qua Out 31, 2012 10:10
por TheKyabu » Qua Out 31, 2012 10:10
Nao consigo interpreta a questao
Seja

, l > 0
a) Calcule a diferencial.
b) Interprete geometricamente o erro que se comete na aproximação de
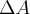
por dA. (Olhe para

como a fórmula para o cálculo da área de quadrado de lado L).
a)
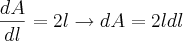
Estou com duvida na hora de encontra o erro quando
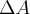
aproxima de dA,tpw usando a formula de
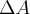
eu chego em


+

^2
mais i ai q interpretaçao devo ter,por favor me ajudem nesse assunto de erro
-
TheKyabu
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Out 19, 2012 19:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por LuizAquino » Qui Nov 01, 2012 16:37
por LuizAquino » Qui Nov 01, 2012 16:37
TheKyabu escreveu:Nao consigo interpreta a questao
Seja

, l > 0
a) Calcule a diferencial.
b) Interprete geometricamente o erro que se comete na aproximação de
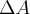
por dA. (Olhe para

como a fórmula para o cálculo da área de quadrado de lado L).
a)
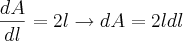
Estou com duvida na hora de encontra o erro quando
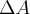
aproxima de dA,tpw usando a formula de
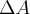
eu chego em


+

^2
mais i ai q interpretaçao devo ter,por favor me ajudem nesse assunto de erro
Você já sabe que

e que

. Você também sabe que por definição temos

. Portanto, temos que

. Comparando então
dA e
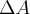
percebemos que a diferença entre eles (que será o erro de aproximação) é

(ou
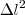
, já que

por definição) . Para entender esse erro geometricamente, analise a figura abaixo.
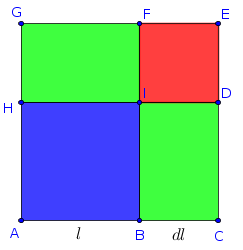
- figura.png (3.34 KiB) Exibido 2225 vezes
Agora responda:
1) Qual é a diferença entre a área do quadrado ABIH e ACEG? (Note que essa diferença representa geometricamente
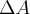
.)
2) Qual é a soma das áreas dos dois retângulos BCDI e IFGH? (Note que essa soma representa geometricamente
dA .)
3) Qual é a área do quadrado IDEF? (Note que essa área representa geometricamente a diferença entre
dA e
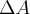
.)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Estimativa do Erro] Aproximação de pi por ...
por e8group » Sex Mai 02, 2014 14:04
- 0 Respostas
- 871 Exibições
- Última mensagem por e8group

Sex Mai 02, 2014 14:04
Cálculo: Limites, Derivadas e Integrais
-
- Aproximação
por Thais Aquino Lima » Qui Fev 28, 2013 19:28
- 1 Respostas
- 1319 Exibições
- Última mensagem por Cleyson007

Sex Mar 01, 2013 09:13
Aritmética
-
- [aproximação linear]
por Giu » Qua Fev 15, 2012 06:09
- 1 Respostas
- 1471 Exibições
- Última mensagem por LuizAquino

Qua Fev 15, 2012 18:26
Cálculo: Limites, Derivadas e Integrais
-
- Aproximação linear
por joaopaulo_ » Sáb Jun 23, 2012 16:59
- 2 Respostas
- 2739 Exibições
- Última mensagem por joaopaulo_

Dom Jun 24, 2012 11:28
Cálculo: Limites, Derivadas e Integrais
-
- Aproximação Linear
por RonnieAlmeida » Sex Mai 23, 2014 00:18
- 0 Respostas
- 1659 Exibições
- Última mensagem por RonnieAlmeida

Sex Mai 23, 2014 00:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , l > 0
, l > 0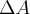 por dA. (Olhe para
por dA. (Olhe para  como a fórmula para o cálculo da área de quadrado de lado L).
como a fórmula para o cálculo da área de quadrado de lado L).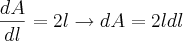
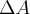 aproxima de dA,tpw usando a formula de
aproxima de dA,tpw usando a formula de 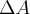

 +
+ ^2
^2

 e que
e que  . Você também sabe que por definição temos
. Você também sabe que por definição temos  . Portanto, temos que
. Portanto, temos que  . Comparando então
. Comparando então  (ou
(ou 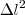 , já que
, já que 
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
