 +140X-2000. Com base nas imformações, responda:
+140X-2000. Com base nas imformações, responda:a) qual o preço que propicia maior lucro? qual é este lucro?
Minha resposta: o melhor preço propicia melhor lucro, então basta calcular o vertice da parabola, ou seja as coordenadas do vertice da parabola, no caso, Xv e Yv ou seja Xv=
 , Yv=
, Yv=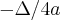 , onde se a=-2 b=140 c=-2000 Yv=R$450,00
, onde se a=-2 b=140 c=-2000 Yv=R$450,00b) Qual o intervalo de preço em que a empresa opera com lucro positivo?
Minha resposta:Apesar de ter uma certa duvida nesta alinea, penso que este intervalo deve ser maior que o valor de c ou seja maior que 2000.
c) Quais os intervalos de preço que fazem a empresa trabalhar no prejuizo?
Minha resposta: aqui acho que tem que ser menor que c.
imagine que subitamente o mercado tornou-se mais exigente, querendo produtos de melhor qualidade. O proprietario descobriu que na nova situação a função que melhor representa o lucro total diario em função do preço de venda é L(X)=5
 +500X+4500.
+500X+4500.d) o que acontecerá se ele continuar vendendo a ração pelo preço definido no item "a"?
e)voce recomendaria um novo preço de venda?qQual?Justifique.)
Por favor acho que sobre estas duas questões estou sem ideias apesar de pedir que me possam esclarecer todas,mais uma vez por favor ajudem me
Filipe


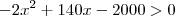



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.