 por Mayra Luna » Ter Out 30, 2012 17:37
por Mayra Luna » Ter Out 30, 2012 17:37
Considere, num sistema cartesiano ortogonal, os pontos A(–1, 3) e B(k, 0). Se o ponto P(4, 5) é equidistante de A e B, então:
A) k = 4
B) k = 2 ou k = 1
C) k = 2 ou k = 6
D) k = 4 ou k = –1
E) k = –1 ou k = 0
Pensei que desse pra fazer com a fórmula da distância entre dois pontos, mas não deu... cheguei à uma equação de 2º grau que tinha resultado com raíz.
Como faço?
-
Mayra Luna
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Out 07, 2012 15:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Ter Out 30, 2012 21:03
por MarceloFantini » Ter Out 30, 2012 21:03
A conta que você precisa resolver é

, portanto
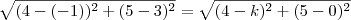
e daí segue que
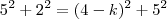
.
Sim, existem duas respostas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Qua Out 31, 2012 22:14
por MarceloFantini » Qua Out 31, 2012 22:14
Você está errando as contas:
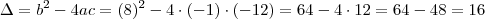
.
Outra forma de resolver:
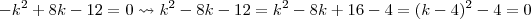
,
daí
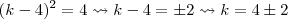
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Mayra Luna » Qua Out 31, 2012 22:25
por Mayra Luna » Qua Out 31, 2012 22:25
Nooooossa! Agora eu vi o que eu estava fazendo, não tinha colocado a equação na ordem certa, tava usando o b como a.
Nem tinha percebido a burrice.
Muito obrigada mesmo!!
-
Mayra Luna
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Out 07, 2012 15:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ponto da reta r que é eqüidistante do ponto A e do ponto B
por gutorocher » Qua Jul 21, 2010 14:01
- 12 Respostas
- 15171 Exibições
- Última mensagem por gutorocher

Sex Jul 23, 2010 13:04
Geometria Analítica
-
- [Vetores] Ponto de reta próximo a outros pares de ponto
por cmcrz97 » Ter Jun 19, 2018 20:29
- 0 Respostas
- 2915 Exibições
- Última mensagem por cmcrz97

Ter Jun 19, 2018 20:29
Álgebra Linear
-
- [Ponto Crítico e Ponto de Inflexão e intervalos] Dúvidas em
por Andre Lopes » Qua Set 26, 2012 00:37
- 2 Respostas
- 3385 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 06:56
Cálculo: Limites, Derivadas e Integrais
-
- Incógnita de logaritmo
por usuariomatematica » Ter Mai 31, 2011 09:18
- 0 Respostas
- 1680 Exibições
- Última mensagem por usuariomatematica

Ter Mai 31, 2011 09:18
Logaritmos
-
- Denominador com incógnita
por TAE » Ter Mai 29, 2012 16:33
- 3 Respostas
- 5734 Exibições
- Última mensagem por Molina

Ter Mai 29, 2012 20:55
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , portanto
, portanto 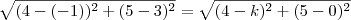 e daí segue que
e daí segue que 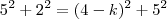 .
.






 ou
ou  daí.
daí.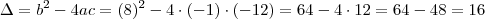 .
.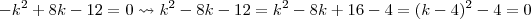 ,
,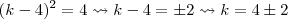 .
.