Há um teorema que diz o seguinte:
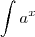



Tentei provar derivando
 , mas não cheguei ao resultado que deveria dar.
, mas não cheguei ao resultado que deveria dar.Fiz o seguinte:
Tentei colocar a parte da regra do quociente em latex aqui, mas deu um "error 6", mas enfim, após montar a regra do quociente e simplificar um pouco, cheguei em:
 , cortando os
, cortando os 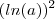 , chego em:
, chego em: , tirando MMC:
, tirando MMC: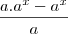 , colocando o a em evidência (na verdade, nem sei se pode):
, colocando o a em evidência (na verdade, nem sei se pode):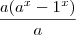 , cortando os a do numerador e denominador, chego em:
, cortando os a do numerador e denominador, chego em:
Sei que há erros aí, por favor me corrijam.



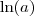 é uma constante, basta derivar
é uma constante, basta derivar 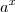 . Note que se
. Note que se  , então
, então 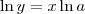 , e pela definição de logaritmo natural, temos que
, e pela definição de logaritmo natural, temos que 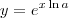 .
.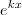 usando a regra da cadeia, portanto
usando a regra da cadeia, portanto  .
. .
.

