Olá Marcela,
Tentarei, passo a passo, explicar uma das maneiras de resolver a inequação:

Primeiramente devemos determinar o domínio. Sabemos que só podemos calcular o logarítmo de números positivos, assim:
Domínio = {x E IR: (x - 1) > 0 e (3x - 2) > 0}
![Domínio=]1,+\infty[ Domínio=]1,+\infty[](/latexrender/pictures/1b1a51203702ac3247866a0836017355.png)
Em seguida, vamos usar algumas propriedades dos logarítmos para simplificar a nossa inequação:

![{log}_{\frac{1}{3}}[(x-1).(3x-2)]\geq-2 {log}_{\frac{1}{3}}[(x-1).(3x-2)]\geq-2](/latexrender/pictures/da18575a0ae1757781c8414f86f94bba.png)


Agora, devemos lembrar que a função
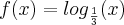
é decrescente. Então:
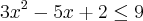
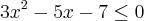
Temos que achar agora as raízes da equação
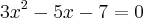
usando a fórmula resolvente. Assim teremos:
![x=\frac{5+\sqrt[]{109}}{6} x=\frac{5+\sqrt[]{109}}{6}](/latexrender/pictures/dabb305f4b159c617cbb9dd03a50a560.png)
ou
![x=\frac{5-\sqrt[]{109}}{6} x=\frac{5-\sqrt[]{109}}{6}](/latexrender/pictures/00534799b3c5fd0635be670c9e9a75a7.png)
De acordo com o domínio, só podemos usar a primeira raíz:
![x=\frac{5+\sqrt[]{109}}{6} x=\frac{5+\sqrt[]{109}}{6}](/latexrender/pictures/dabb305f4b159c617cbb9dd03a50a560.png)
Finalmente, vamos construir o quadro de sinais (ver anexo) e assim determinar o intervalo, dentro do nosso domínio, onde
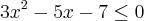
Portanto, de acordo com o quadro de sinais, a solução da nossa inequação é o intervalo:
![]1, \frac{5+\sqrt[]{109}}{6}] ]1, \frac{5+\sqrt[]{109}}{6}]](/latexrender/pictures/84fcd32ceb2f04f7b83f61682d82baf8.png)
Como sempre, devemos fazer a verificação. Por exemplo, escolhemos x = 2. Assim:
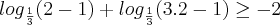
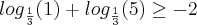
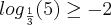

Verificamos assim que a solução da nossa inequação é o intervalo:
![]1, \frac{5+\sqrt[]{109}}{6}] ]1, \frac{5+\sqrt[]{109}}{6}]](/latexrender/pictures/84fcd32ceb2f04f7b83f61682d82baf8.png)
Espero ter ajudado e até breve!




![Domínio=]1,+\infty[ Domínio=]1,+\infty[](/latexrender/pictures/1b1a51203702ac3247866a0836017355.png)

![{log}_{\frac{1}{3}}[(x-1).(3x-2)]\geq-2 {log}_{\frac{1}{3}}[(x-1).(3x-2)]\geq-2](/latexrender/pictures/da18575a0ae1757781c8414f86f94bba.png)


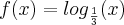 é decrescente. Então:
é decrescente. Então: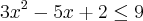
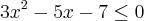
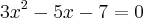 usando a fórmula resolvente. Assim teremos:
usando a fórmula resolvente. Assim teremos:![x=\frac{5+\sqrt[]{109}}{6} x=\frac{5+\sqrt[]{109}}{6}](/latexrender/pictures/dabb305f4b159c617cbb9dd03a50a560.png) ou
ou ![x=\frac{5-\sqrt[]{109}}{6} x=\frac{5-\sqrt[]{109}}{6}](/latexrender/pictures/00534799b3c5fd0635be670c9e9a75a7.png)
![x=\frac{5+\sqrt[]{109}}{6} x=\frac{5+\sqrt[]{109}}{6}](/latexrender/pictures/dabb305f4b159c617cbb9dd03a50a560.png)
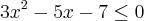
![]1, \frac{5+\sqrt[]{109}}{6}] ]1, \frac{5+\sqrt[]{109}}{6}]](/latexrender/pictures/84fcd32ceb2f04f7b83f61682d82baf8.png)
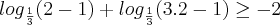
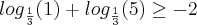
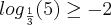

![]1, \frac{5+\sqrt[]{109}}{6}] ]1, \frac{5+\sqrt[]{109}}{6}]](/latexrender/pictures/84fcd32ceb2f04f7b83f61682d82baf8.png)



 , avisa que eu resolvo.
, avisa que eu resolvo.

