[Aplicação e Otimização de derivadas] Custo, receita e lucro

por **ricael** » Ter Out 23, 2012 11:21

Pessoal nao consigo chegar na resposta desse problema de otmização, se puder um passo a passo agradeço

Se r(x) é a receita proveniente da venda de x ?tens, c(x) é o custo da produção de x ?tens e p(x) = r(x) ? c(x) é o lucro sobre a venda de x ?tens, então, o retorno (receita), o custo e o lucro marginais
provenientes desse n?vel de produção (x ?tens) são dados, respectivamente por dr/dx, dc/dx, dp/dx. Suponha que
r(x) = 9x, c(x) = x³ ? 6x² + 15x, em que x representa milhares de unidades. Há um nivel de
produção que maximize o lucro? Se houver, qual é? Há um nivel de produção que minimize o custo?

R: Sim: x = 2 + ?2 mil unidades ou x = 2 ? ?2 mil unidades. Não

por **young_jedi** » Ter Out 23, 2012 12:22

pegando a função do lucro teriamos

p(x)=9x-x^3+6x^2-15x

para encontrar valores de maximos e minimos desta função utilizamos a derivada primeira e igualamos a 0

p'(3)=-3x^2+12x-6

aplicando baskara

$x_1=2-\sqrt{2}$

$x_2=2+\sqrt{2}$

mais não sabemos qual é ponto de maximo e qual é de minimo, portanto aplicamos a derivada segunda nestes pontos

p''(x)=-6x+12

$p''(2-\sqrt{2})=-6(2-\sqrt{2})+12$

$p''(2-\sqrt{2})=-12+6\sqrt{2}+12=6\sqrt{2}$

como este valor é maior que zero então indica que este é um ponto de minimo

pra o outro valor

p''(x)=-6x+12

$p''(2+\sqrt{2})=-6(2+\sqrt{2})+12$

$p''(2+\sqrt{2})=-12-6\sqrt{2}+12=-6\sqrt{2}$

como valor é negativo isto indica um ponto de maximo

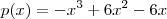
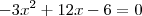
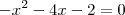
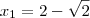
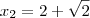
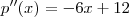
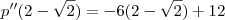
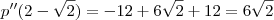
portanto $x=2+\sqrt{2}$ é um valor que maximiza o lucro

tente aplicar o mesmo raciocinio para a função de custo c(x) e veja os pontos que encontra.

por **ricael** » Ter Out 23, 2012 16:25

Muito obrigado young_jedi
vc salvo meus estudos, passei dois dias tentando fazer e vi que meu erro tava em nao fazer a segunda derivada, muito obrigado mesmo!