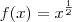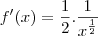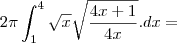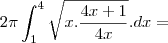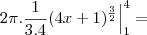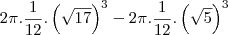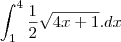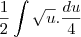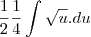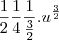por ariclenesmelo » Seg Out 22, 2012 22:00
por ariclenesmelo » Seg Out 22, 2012 22:00
Estou com a seguinte questão..
Inicialmente e esboçada em um plano cartesiano, a função com seus limites que dará o formato da peça, posteriormente, ocorre uma rotação em um de seus eixos, formando-a. Ocorreu uma rotação em x da função f(x)= Raiz X ou x^1/2, que foi limitada pelos pontos (1,1) e (4,2), pode-se concluir que a area da figura formada e: considere raiz 17 = 4,1 raiz 5 = 2,2 e PI= 3,14..
Alternativas .. A) 30 u.a B) 30.7 u.a C) 31,4 u.a D) 31,8 u.a E) 32,6 u.a
Tentei de tudo mais não consigo chegar a nenhum desses valores.. Gostaria da ajuda de vocês..
-
ariclenesmelo
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Out 22, 2012 21:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas para Internet
- Andamento: formado
 por young_jedi » Seg Out 22, 2012 23:25
por young_jedi » Seg Out 22, 2012 23:25
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por ariclenesmelo » Ter Out 23, 2012 00:24
por ariclenesmelo » Ter Out 23, 2012 00:24
Amigo, muito Obrigado por sua ajuda, a resposta esta correta, só tenho uma duvida, como chegou a solução do penúltimo parágrafo 1/3x4 pois o resto eu consegui entender, acompanhei o passo a passo pelo wolframalpha e ele diferentemente chegou ao 1/8 x 2/3 que resumindo chegaria na mesma solução que você 1/12 . Poderia me ajudar a chegar nessa sua solução de 1/3x4.. desde já agradeço sua ajuda.
-
ariclenesmelo
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Out 22, 2012 21:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas para Internet
- Andamento: formado
 por young_jedi » Ter Out 23, 2012 11:37
por young_jedi » Ter Out 23, 2012 11:37
Opa, amigo sem problemas
pelo que entendi é na parte da integração certo?
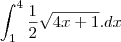
primeiro eu coloquei o 1/2 pra fora da integral

utilizei integração por substituição de variaveis


substituindo
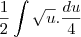
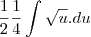
intergrando
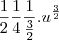
voltando para variavel x e simplificando

acredito que seja isso
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Area de uma superficie de revolução
por miumatos » Seg Jun 18, 2012 01:34
- 1 Respostas
- 1976 Exibições
- Última mensagem por LuizAquino

Ter Jun 19, 2012 11:05
Cálculo: Limites, Derivadas e Integrais
-
- Rotação-Superficie de Revolução
por DGM » Ter Dez 05, 2017 00:37
- 0 Respostas
- 1789 Exibições
- Última mensagem por DGM

Ter Dez 05, 2017 00:37
Geometria Analítica
-
- [Integral polar] Superfície de revolução
por Paulo Perez » Sex Out 17, 2014 15:16
- 3 Respostas
- 2500 Exibições
- Última mensagem por Paulo Perez

Sex Out 17, 2014 18:09
Cálculo: Limites, Derivadas e Integrais
-
- [Aplicação de Integral] Área de Revolução
 por carlosce88 » Qua Out 26, 2016 22:40
por carlosce88 » Qua Out 26, 2016 22:40
- 0 Respostas
- 5059 Exibições
- Última mensagem por carlosce88

Qua Out 26, 2016 22:40
Cálculo: Limites, Derivadas e Integrais
-
- área da superfície
por martinay » Sáb Out 29, 2011 02:52
- 1 Respostas
- 1307 Exibições
- Última mensagem por LuizAquino

Sáb Out 29, 2011 10:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.