 por Fabio Wanderley » Seg Out 22, 2012 18:10
por Fabio Wanderley » Seg Out 22, 2012 18:10
Boa tarde!
Segue o exemplo:
Seja f uma função ímpar e contínua em [-r,r], r > 0. Mostre que:
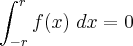
Solução:
f ímpar <-> f(-x) = -f(x) em [-r,r].
Façamos a mudança de variável u = -x
u = - x; du = - dx
x = - r; u = r
x = r; u = - r

Como f(- u) = - f(u), resulta
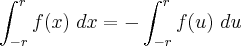 (<--- até aqui tudo bem)
(<--- até aqui tudo bem)mas,

(veja observação acima), logo:
(<--- não entendi isso)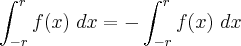
(...)
Guidorizzi, p. 322, vol. 1, 5 ed.Estou entendo até chegar a linha que marquei. Depois não consigo entender como ele concluiu a igualdade... e como assim "veja observação acima"? Para mim ficou confuso.
Alguém pode me ajudar?
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por young_jedi » Seg Out 22, 2012 18:40
por young_jedi » Seg Out 22, 2012 18:40
repare que as duas exprresões representam a mesma integral, apenas se utilizou outro simbolo para representar a variavel
poderia utilizar qualquer simbolo, note que;
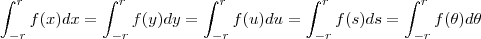
é apenas o simbolo da variavel que é diferente mais representam a mesma integral
por isso ele pode fazer a igualdade
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Fabio Wanderley » Seg Out 22, 2012 19:59
por Fabio Wanderley » Seg Out 22, 2012 19:59
young_jedi escreveu:repare que as duas exprresões representam a mesma integral, apenas se utilizou outro simbolo para representar a variavel
poderia utilizar qualquer simbolo, note que;
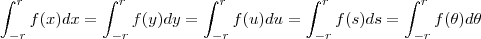
é apenas o simbolo da variavel que é diferente mais representam a mesma integral
por isso ele pode fazer a igualdade
young_jedi,
Mas se ele definiu que u = - x
e conclui que
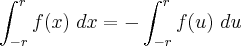
como logo depois ele coloca que
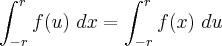
???
Não estou conseguindo enxergar como "sumiu" o sinal negativo de um lado da equação...
Agradeço desde já sua atenção!
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por young_jedi » Seg Out 22, 2012 21:31
por young_jedi » Seg Out 22, 2012 21:31
a questão é que as duas igualdades são verdadeiras
a primeira igualdade ele tirou do fato da função ser impar e continua como voce demonstrou
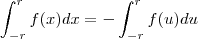
a segunda ele tirou do fato de ser possivel fazer a substituição que eu desmonstrei
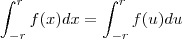
sendo assim as duas igualdades são verdadeiras com isso então nos temos que

mais isso só é possivel se

sendo assim demosntramos aquilo que se queria desde o inicio
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Fabio Wanderley » Seg Out 22, 2012 21:48
por Fabio Wanderley » Seg Out 22, 2012 21:48
Obrigado, young_jedi!
Tinha dado um tempo pra essa questão e voltei agora para vê-la novamente... ficou melhor pra entender

Acho que vou usá-la numa apresentação...
abraço!
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda interpretação
por deividchou » Seg Ago 17, 2015 12:53
- 3 Respostas
- 4072 Exibições
- Última mensagem por AlexCA68

Sáb Mar 12, 2016 14:37
Aritmética
-
- [Limite] Ajuda com demonstração
por ghf » Sex Nov 02, 2012 22:31
- 1 Respostas
- 1479 Exibições
- Última mensagem por MarceloFantini

Sex Nov 02, 2012 22:39
Cálculo: Limites, Derivadas e Integrais
-
- [Equação Diferencial]Ajuda num passo de uma demonstração
por Bravim » Qui Abr 09, 2015 18:14
- 0 Respostas
- 791 Exibições
- Última mensagem por Bravim

Qui Abr 09, 2015 18:14
Cálculo: Limites, Derivadas e Integrais
-
- Interpretação dos Monômios
por Jhenrique » Sáb Nov 10, 2012 18:57
- 8 Respostas
- 6771 Exibições
- Última mensagem por Jhenrique

Ter Jan 01, 2013 17:31
Álgebra Elementar
-
- Interpretação dessa questão
por Joelson » Dom Jun 21, 2009 17:22
- 2 Respostas
- 2931 Exibições
- Última mensagem por Joelson

Dom Jun 21, 2009 19:13
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
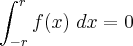

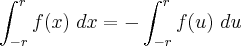 (<--- até aqui tudo bem)
(<--- até aqui tudo bem) (veja observação acima), logo: (<--- não entendi isso)
(veja observação acima), logo: (<--- não entendi isso)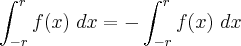


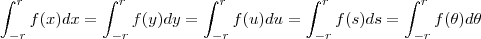

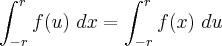
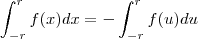
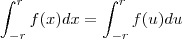




 , avisa que eu resolvo.
, avisa que eu resolvo.

