 por tiaguito » Seg Out 22, 2012 17:01
por tiaguito » Seg Out 22, 2012 17:01
Tenho aqui comigo, um exercício de funções, quero resolver pois tenho prova semana que vem e não estou sabendo como desenvolver os cálculos.. não to aqui para pedir respostas, só quero entender como eu posso fazer o seguinte exercício, que formula e que dados posso utilizar para resolver o mesmo. A seguir o exercício.
Em algumas regiões do Brasil, as tomas elétricas padrão fornecem uma corrente elétrica senoidal com uma voltagem máxima de V= 120raizde2 volts(v), a uma frequência de 60 ciclos por segundo.
então os dados que tenho é V= 120raisde2 e a frequência 60s e pede para escrever a equação que expressa V como função do tempo dai diz que V=0 em T=0
que equação eu posso utilizar para resolver esse exercício? Quero muito saber resolver esta questão. Muito Obrigado

-
tiaguito
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 22, 2012 16:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por Russman » Seg Out 22, 2012 18:35
por Russman » Seg Out 22, 2012 18:35
tiaguito escreveu:Em algumas regiões do Brasil, as tomas elétricas padrão fornecem uma corrente elétrica senoidal com uma voltagem máxima de V= 120raizde2 volts(v), a uma frequência de 60 ciclos por segundo.
A palavra chave é
senoidal. Uma função senoidal é do tipo
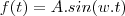
onde chamamos
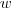
de frequência angular e é possível mostrar que

é o valor máximo dessa função.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dificuldade para resolver esse sistema.
por 380625 » Sáb Ago 20, 2011 16:08
- 1 Respostas
- 5801 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 00:32
Sistemas de Equações
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4611 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- Probleminha de funções, preciso de ajuda para resolver.
por d4rwin » Ter Ago 18, 2015 01:31
- 8 Respostas
- 5676 Exibições
- Última mensagem por nakagumahissao

Ter Ago 18, 2015 19:52
Funções
-
- funções lista ajuda para resolver não sei como fazer
por flesh555 » Sáb Fev 16, 2013 10:18
- 0 Respostas
- 1575 Exibições
- Última mensagem por flesh555

Sáb Fev 16, 2013 10:18
Funções
-
- Dificuldade em resolver o exercicio nº 2
por Catriane Moreira » Sáb Nov 20, 2010 23:01
- 1 Respostas
- 2169 Exibições
- Última mensagem por alexandre32100

Seg Nov 22, 2010 14:42
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



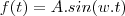
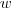 de frequência angular e é possível mostrar que
de frequência angular e é possível mostrar que  é o valor máximo dessa função.
é o valor máximo dessa função.
