Uma construtora deseja cercar um terreno de 1000m² para sua sede, em três de seus lados, deixando o quarto lado para a construção. Seu objetivo como Engenheiro é projetar isso, de forma a usar o mínimo de muro.
A) Sejam x e y as dimensões do tereno e L o comprimento da cerca requerido para cercar aquelas dimensões. Como a área é de 1000m², devemos ter xy=1000. Ache uma fórmula para L em termos de x e de y e então expresse L em termos só de x usando a quação da área.
B) Há restrições sobre os valores de x? Justifique.
Por faor me ajudem a resolver essa questão.
é o comprimento requerido da cerca do terreno então este é o perímetro do mesmo. Logo, 
, supondo que o terreno seja retangular e que o lado sem cerca seja o de comprimento 
.
de onde , isoladamente, os valores de 
são dados por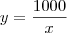 
. Dessa forma,
o valor do perímetro não se define. Logo, existe a restrição 
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")