por cristian9192 » Sáb Out 20, 2012 15:06
por cristian9192 » Sáb Out 20, 2012 15:06
Já tentei fazer essa integral dupla definida varias vezes só que sempre me perco na troca de variaveis:
![\int_{-3}^{3}\int_{-\sqrt[2]{9-x^2}}^{\sqrt[2]{9-x^2}}{e}^{-x^2-y^2} dy dx \int_{-3}^{3}\int_{-\sqrt[2]{9-x^2}}^{\sqrt[2]{9-x^2}}{e}^{-x^2-y^2} dy dx](/latexrender/pictures/f48688073a97bebc92696b9c537f848f.png)
Se alguém poder me ajudar.
Desde já agradeço!
-
cristian9192
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sex Out 19, 2012 02:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Sáb Out 20, 2012 15:59
por young_jedi » Sáb Out 20, 2012 15:59
temos que pelos limites de integração

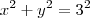
então essa integral é efetuada sobre um circulo de raio igual a 3
então mudando para cooredenadas polares

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por cristian9192 » Sáb Out 20, 2012 18:50
por cristian9192 » Sáb Out 20, 2012 18:50
Valeu cara, consegui fazer o resto da integral.
-
cristian9192
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sex Out 19, 2012 02:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral dupla
por DanielFerreira » Sex Mar 16, 2012 23:56
- 2 Respostas
- 2867 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 17, 2012 19:11
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 2
por DanielFerreira » Dom Mar 18, 2012 12:44
- 5 Respostas
- 4150 Exibições
- Última mensagem por DanielFerreira

Sex Mar 23, 2012 22:34
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 4
 por DanielFerreira » Sex Abr 06, 2012 19:49
por DanielFerreira » Sex Abr 06, 2012 19:49
- 4 Respostas
- 3127 Exibições
- Última mensagem por DanielFerreira

Sex Abr 06, 2012 21:05
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 5
por DanielFerreira » Sex Abr 06, 2012 20:00
- 2 Respostas
- 1912 Exibições
- Última mensagem por DanielFerreira

Sex Abr 06, 2012 20:16
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 6
 por DanielFerreira » Sáb Abr 14, 2012 22:54
por DanielFerreira » Sáb Abr 14, 2012 22:54
- 1 Respostas
- 1627 Exibições
- Última mensagem por LuizAquino

Dom Abr 15, 2012 23:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{-3}^{3}\int_{-\sqrt[2]{9-x^2}}^{\sqrt[2]{9-x^2}}{e}^{-x^2-y^2} dy dx \int_{-3}^{3}\int_{-\sqrt[2]{9-x^2}}^{\sqrt[2]{9-x^2}}{e}^{-x^2-y^2} dy dx](/latexrender/pictures/f48688073a97bebc92696b9c537f848f.png)

![\int_{-3}^{3}\int_{-\sqrt[2]{9-x^2}}^{\sqrt[2]{9-x^2}}{e}^{-x^2-y^2} dy dx \int_{-3}^{3}\int_{-\sqrt[2]{9-x^2}}^{\sqrt[2]{9-x^2}}{e}^{-x^2-y^2} dy dx](/latexrender/pictures/f48688073a97bebc92696b9c537f848f.png)