Observe a figura:
http://pir2.forumeiros.com/t9704-funcoes-duvidas#125945
Nessa figura, está representada a parábola de vértice V, gráfico da função de segundo grau cuja expressão é
a) y = (x2 /5) - 2x
b) y = x2 - 10x
c) y = x2 + 10x
d) y = (x2/5) - 10x
e) y = (x2/5) + 10x
Por gentileza alguem pode me ajudar! Não estou entendo desta parte em diante:
Na figura temos o ponto (5,-5), ou seja:
1. Como: 5a + b = ficou -1
OBS; DESTA PARTE EM DIANTE NAO CONSIGO MAIS ENTENDER.


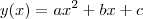
 ,
, e
e  .
.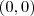 e
e  . Assim,
. Assim,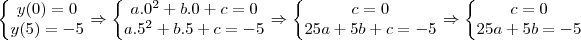
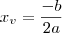 de modo que
de modo que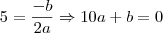
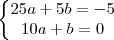 .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

