 por Sherminator » Sáb Out 20, 2012 09:59
por Sherminator » Sáb Out 20, 2012 09:59
Bom dia, podiam-me ajudar a resolver esta equação, se faz favor.
x + 2y - z =1
2x - 3y + 6z =2
3x - y + 7z =5
-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por e8group » Sáb Out 20, 2012 10:29
por e8group » Sáb Out 20, 2012 10:29
O raciocínio é este (não o único ) :
i) Isole uma incógnita (x,y ou z ) da primeira equação .
ii) Substitua o mesmo na segunda equação .( Com isso a segunda equação terá 2 incógnitas ) .
iii) Faça o mesmo processo que em i) ,mas lembre-se que será na segunda equação .
iv) Faça o mesmo processo que em ii) na equação três e isole está incógnita que terá o valor dela . Daí você substitui este valor nas demais equações .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Sherminator » Sáb Out 20, 2012 11:46
por Sherminator » Sáb Out 20, 2012 11:46
Obrigado pela ajuda Santhiago, mas mesmo assim não consegui resolver pois ficou em fracção a uma certa altura, dá para colocar aqui o exercício resolvido se faz favor?
-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por e8group » Sáb Out 20, 2012 12:26
por e8group » Sáb Out 20, 2012 12:26

1)
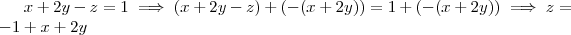
2)

Note que a segunda equação ,pode ser escrita como
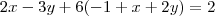
Pois

.
Assim ,
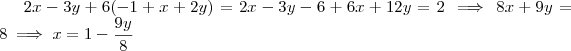
3) Analogamente como em 1 e 2 ,

Resolvendo ,fica
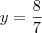
.
Lembrando que ,

e

,basta susbstituir y em cada equação .
Depois vc testa os valores , se sastifazer todas equações a solução estar correta .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Sherminator » Sáb Out 20, 2012 13:00
por Sherminator » Sáb Out 20, 2012 13:00
-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sistema com 15 equações e 15 incógnitas
por Bruhh » Seg Set 06, 2010 16:02
- 3 Respostas
- 3558 Exibições
- Última mensagem por MarceloFantini

Qui Set 09, 2010 14:56
Álgebra Linear
-
- Sistema de Equaçoes com 3 Incognitas
por -Ricke » Qui Mar 17, 2011 20:26
- 1 Respostas
- 4732 Exibições
- Última mensagem por DanielFerreira

Qua Mar 23, 2011 14:55
Sistemas de Equações
-
- Sistema de 2 equações com 3 incógnitas
por Jessiica » Dom Nov 11, 2012 16:22
- 1 Respostas
- 9719 Exibições
- Última mensagem por CaptainObvious

Dom Nov 11, 2012 17:16
Sistemas de Equações
-
- SISTEMA COM 3 INCÓGNITAS !!
por mateuscastelo » Dom Out 28, 2012 00:56
- 1 Respostas
- 1972 Exibições
- Última mensagem por young_jedi

Dom Out 28, 2012 18:09
Sistemas de Equações
-
- Sistema de equacao com 2 incognitas
por -Rafael- » Qua Fev 29, 2012 13:23
- 2 Respostas
- 1744 Exibições
- Última mensagem por -Rafael-

Qua Fev 29, 2012 15:01
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






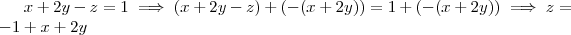

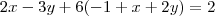
 .
. 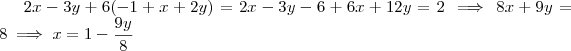

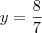 .
.  e
e  ,basta susbstituir y em cada equação .
,basta susbstituir y em cada equação .





