 por Milton21 » Qui Out 18, 2012 15:14
por Milton21 » Qui Out 18, 2012 15:14
Calcular a e b de modo que sejam colineares os pontos A(3,1,-2), B(1,5,1) e C(a,b,7)
Eu fiz fazendo uma matriz e deu a seguinte expressao: 98 + 11a - 5b
como eu desenvolvo? brigado
-
Milton21
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Out 18, 2012 15:09
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Qui Out 18, 2012 16:12
por e8group » Qui Out 18, 2012 16:12
Pensei assim :
Se os pontos A,B e C são colineares ,podemos dizer que
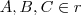
,isto é , os três pontos pertence a uma mesma reta (r) . Através dos pontos , temos que os vetores AB e BC são paralelos .Ou seja, suas componentes são proporcionais .Assim ,
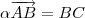
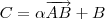
.
Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Milton21 » Qui Out 18, 2012 18:03
por Milton21 » Qui Out 18, 2012 18:03
O 'B' nao passaria dividindo ao inves de somando?
-
Milton21
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Out 18, 2012 15:09
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Sex Out 19, 2012 17:18
por e8group » Sex Out 19, 2012 17:18
Milton21 escreveu:O 'B' nao passaria dividindo ao inves de somando?
Não , note que
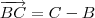
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Sex Out 19, 2012 17:48
por e8group » Sex Out 19, 2012 17:48
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Pontos Não-Colineares
 por wilgaroto » Sex Out 28, 2011 09:41
por wilgaroto » Sex Out 28, 2011 09:41
- 1 Respostas
- 4453 Exibições
- Última mensagem por LuizAquino

Sáb Out 29, 2011 11:51
Geometria Analítica
-
- Pontos Colineares
por Claudin » Qui Abr 05, 2012 19:19
- 3 Respostas
- 10680 Exibições
- Última mensagem por Claudin

Qui Abr 05, 2012 22:31
Geometria Analítica
-
- Pontos P,Q e R - Colineares ?
por PeterHiggs » Seg Set 24, 2012 19:10
- 2 Respostas
- 2455 Exibições
- Última mensagem por PeterHiggs

Ter Set 25, 2012 13:18
Geometria Espacial
-
- Duvida Pontos Colineares
por samuel_corf » Seg Abr 25, 2011 11:51
- 4 Respostas
- 9502 Exibições
- Última mensagem por LuizAquino

Dom Jul 24, 2011 20:46
Matrizes e Determinantes
-
- Combinaçao com elementos colineares
por rsholtermann » Qua Jul 14, 2010 13:21
- 1 Respostas
- 3052 Exibições
- Última mensagem por MarceloFantini

Qua Jul 14, 2010 14:50
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



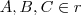 ,isto é , os três pontos pertence a uma mesma reta (r) . Através dos pontos , temos que os vetores AB e BC são paralelos .Ou seja, suas componentes são proporcionais .Assim ,
,isto é , os três pontos pertence a uma mesma reta (r) . Através dos pontos , temos que os vetores AB e BC são paralelos .Ou seja, suas componentes são proporcionais .Assim ,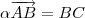
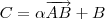 .
.

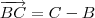 .
.
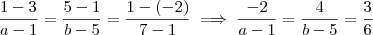


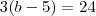



 .
.
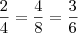 .OK!.
.OK!.


 , avisa que eu resolvo.
, avisa que eu resolvo.

