Encontre a equação da reta tangente à curva
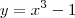 , que seja perpendicular à reta
, que seja perpendicular à reta 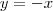 .
.Sei que a equação base da reta tangente é
 e que m é o coeficiente angular, ou seja, a derivada de uma função em certo ponto. Para encontrar m, eu derivei o y, ficando:
e que m é o coeficiente angular, ou seja, a derivada de uma função em certo ponto. Para encontrar m, eu derivei o y, ficando: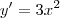 , mas como não tenho um ponto específico, não sei achar o valor de m (coeficiente angular).
, mas como não tenho um ponto específico, não sei achar o valor de m (coeficiente angular).Sei pegar um ponto desta reta, seria: P(1,-1).
Como faço pra prosseguir com o exercício?


 . Para perceber isto, lembre-se do fato que
. Para perceber isto, lembre-se do fato que 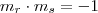 , onde
, onde 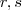 são retas perpendiculares.
são retas perpendiculares.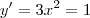 , assim
, assim  . Logo teremos que a reta tangente à curva será perpendicular em dois pontos distintos.
. Logo teremos que a reta tangente à curva será perpendicular em dois pontos distintos.


 .
.



