2x-y = 7
x+4y=-1
Então fiz assim
8x-4y=7
4x=7
x=7-4
x=3
Não entendo muito como resolve sistema então fiz assim,mas não estou sabendo resolver para achar o outro valor.
Se estiver errado fazer assim,pelo menos achei o valor de um deles.kkkkk


GABRIELA escreveu:Estou com a seguinte questão de sistema:
2x-y = 7
x+4y=-1
Então fiz assim
8x-4y=7
4x=7
x=7-4
x=3
Não entendo muito como resolve sistema então fiz assim,mas não estou sabendo resolver para achar o outro valor.
Se estiver errado fazer assim,pelo menos achei o valor de um deles.kkkkkTentei!!!
 (equação 1)
(equação 1)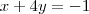 (equação 2)
(equação 2) pelo valor encontrado no item 1).
pelo valor encontrado no item 1).

molina escreveu:GABRIELA escreveu:Estou com a seguinte questão de sistema:
2x-y = 7
x+4y=-1
Então fiz assim
8x-4y=7
4x=7
x=7-4
x=3
Não entendo muito como resolve sistema então fiz assim,mas não estou sabendo resolver para achar o outro valor.
Se estiver errado fazer assim,pelo menos achei o valor de um deles.kkkkkTentei!!!
Boa noite, Gabriela.
Em sistemas lineares os mesmo valores de x e y encontrados tem que satisfazer ambas equações.
Um dos modos mais fáceis e usados para resolver isso é isolar uma incognita (x ou y) em uma das equações e substituir o valor correspondente na outra equação, ficando assim com apenas uma variável. Assim:(equação 1)
(equação 2)
1) Isole o x da equação 2, ou seja, deixa x sozinho de um lado do igual e o restante do outro lado.
2) Na equação 1 subtitua o x que está junto com opelo valor encontrado no item 1).
3) Com isso você vai ficar apenas com y na equação, sendo possível determinar o valor dele.
4) Com o valor de y achado, substitua em qualquer uma das equações e encontre o valor de x.
Tente e comente qualquer novidade.
Até mais.


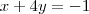

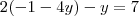
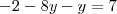
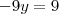
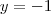




molina escreveu:
Substituindo:
Você pode verificar se os valores são corretos substituindo-os nas duas equações.
Faça isso!

GABRIELA escreveu:molina escreveu:
Substituindo:
Você pode verificar se os valores são corretos substituindo-os nas duas equações.
Faça isso!
Ok! Entendi como resolve um sistema desse.
Obrigada!
Mas agora eu tenho um sistema que tem 3 equações.
Veja:
x + x + z = -1
2x - y - 3z = 5
x + 2y + z = 0
O procedimento não vai ser o mesmo da anterior,vai?
GABRIELA escreveu:
x + x + z = -1
2x - y - 3z = 5
x + 2y + z = 0
 (mudei aqui!)
(mudei aqui!)



molina escreveu:GABRIELA escreveu:molina escreveu:
Substituindo:
Você pode verificar se os valores são corretos substituindo-os nas duas equações.
Faça isso!
Ok! Entendi como resolve um sistema desse.
Obrigada!
Mas agora eu tenho um sistema que tem 3 equações.
Veja:
x + x + z = -1
2x - y - 3z = 5
x + 2y + z = 0
O procedimento não vai ser o mesmo da anterior,vai?
Olá, Gabriela.
Para perguntas diferentes, tópicos diferentes, ok? Então nas próximas crie um novo tópico. Mas essa vou responder aqui:
O procedimento é diferente do anterior. Durante seus estudos você vai ver diferentes maneiras de encontrar a mesma coisa (no caso, de encontrar x, y e z).
Por agora, não posso lhe ajudar, pois não sei qual ferramentas você ja viu nas aulas. Escalonamento? Cramer?
Aproveito aqui já para corrigir seu erro de digitação:GABRIELA escreveu:
x + x + z = -1
2x - y - 3z = 5
x + 2y + z = 0
Correto:(mudei aqui!)

Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: