Álgebra Linear

[marinalcd]

Como faço para determinar se uma transformação linear é injetora ou sobrejetora?
Por exemplo: T(x,y)= (x-2y,3x+y,x+y) é injetora ou sobrejetora.
Não estou conseguindo determinar!

[young_jedi]

uma transformação é dita injetora se elementos distintos do dominio fornecem imagens distintas.

ou seja para um dado existe uma imagem sendo que nenhum outro par (x,y) resulte nessa mesma imagem.
observe que se existirem dois elementos do dominio que tem a mesma imagem podemos dizer





dai tiramos





temos que a unica solução deste sistema sera para




ou seja




sendo assim eles são o mesmo elemento, portanto cada elemento da imagem possui apenas um elemento correpondente no dominio então a função é injetora.
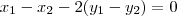
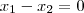
para a função sobrejetora lembre-se de que a imagem deve ser igual ao contra-dominio, neste caso o contradominio são os elementos de , então voce tem que verificar se para cada elemento de existe um par (x,y) associado a ele.

[marinalcd]

Obrigada pela ajuda!

Então, sendo uma função injetora, ela não pode ser sobrejetora, né? (nesse caso)
Mesmo eu calculando.

[young_jedi]

uma função pode sim ser sobrejetora e injetora sendo assim bijetora, não é o caso desta
ela é injetora porem não e sobrejetora.

[marinalcd]

Muito obrigada pela ajuda!!