 por Jessica Seno » Seg Out 15, 2012 11:14
por Jessica Seno » Seg Out 15, 2012 11:14
Bom Dia,
Eu comecei a integrar:
![\int_{}^{}\frac{xdx}{\sqrt[]{x+1}}} \int_{}^{}\frac{xdx}{\sqrt[]{x+1}}}](/latexrender/pictures/bcf4d19f66711a9783486e9b54844980.png)
Chamei u=x+1=> x=u-1
Logo, dx=du.
Daí,
![\int_{}^{}\frac{xdx}{\sqrt[]{x+1}}=\int_{}^{}\frac{\left(u-1 \right)du}{\sqrt[]{u}} \int_{}^{}\frac{xdx}{\sqrt[]{x+1}}=\int_{}^{}\frac{\left(u-1 \right)du}{\sqrt[]{u}}](/latexrender/pictures/b626a1909772cf1f927a39471e951c56.png)
Estou no caminho certo ou existe um mais fácil?... Empaquei aí...
-
Jessica Seno
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Out 14, 2012 14:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por young_jedi » Seg Out 15, 2012 15:24
por young_jedi » Seg Out 15, 2012 15:24
sua solução esta certa, oque voce precisa fazer é escrever a integral de um jeito mais facil

podemos ainda melhorar mais
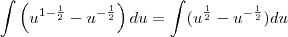
a partir dai é so aplicar o conceito de anti derivada.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Jessica Seno » Ter Out 16, 2012 08:56
por Jessica Seno » Ter Out 16, 2012 08:56
Bom Dia,
Muito obrigada pela ajuda...
Agora deu certo...
Jéssica Seno
-
Jessica Seno
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Out 14, 2012 14:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Dúvida com uma integral simples
por Leonardo Ribeiro » Sex Abr 03, 2015 20:02
- 1 Respostas
- 2083 Exibições
- Última mensagem por Leonardo Ribeiro

Sex Abr 03, 2015 21:06
Cálculo: Limites, Derivadas e Integrais
-
- [integral] duvida integral
por lucasdemirand » Ter Nov 26, 2013 17:47
- 0 Respostas
- 905 Exibições
- Última mensagem por lucasdemirand

Ter Nov 26, 2013 17:47
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em Integral
por Cleyson007 » Ter Fev 28, 2012 17:36
- 5 Respostas
- 2194 Exibições
- Última mensagem por LuizAquino

Qui Mar 01, 2012 16:27
Cálculo: Limites, Derivadas e Integrais
-
- Duvida na Integral
por rodrigo ff » Sex Mar 23, 2012 17:44
- 1 Respostas
- 1534 Exibições
- Última mensagem por DanielFerreira

Sex Mar 23, 2012 19:01
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] - Dúvida
por digsydinner » Ter Mar 27, 2012 10:37
- 3 Respostas
- 1865 Exibições
- Última mensagem por LuizAquino

Sex Mar 30, 2012 00:07
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\frac{xdx}{\sqrt[]{x+1}}} \int_{}^{}\frac{xdx}{\sqrt[]{x+1}}}](/latexrender/pictures/bcf4d19f66711a9783486e9b54844980.png)
![\int_{}^{}\frac{xdx}{\sqrt[]{x+1}}=\int_{}^{}\frac{\left(u-1 \right)du}{\sqrt[]{u}} \int_{}^{}\frac{xdx}{\sqrt[]{x+1}}=\int_{}^{}\frac{\left(u-1 \right)du}{\sqrt[]{u}}](/latexrender/pictures/b626a1909772cf1f927a39471e951c56.png)

![\int_{}^{}\frac{xdx}{\sqrt[]{x+1}}} \int_{}^{}\frac{xdx}{\sqrt[]{x+1}}}](/latexrender/pictures/bcf4d19f66711a9783486e9b54844980.png)
![\int_{}^{}\frac{xdx}{\sqrt[]{x+1}}=\int_{}^{}\frac{\left(u-1 \right)du}{\sqrt[]{u}} \int_{}^{}\frac{xdx}{\sqrt[]{x+1}}=\int_{}^{}\frac{\left(u-1 \right)du}{\sqrt[]{u}}](/latexrender/pictures/b626a1909772cf1f927a39471e951c56.png)


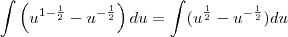



 .
.
 :
: