Geometria

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Geometria

Regras do fórum
Responder

Geometria

Mensagempor RafahAparecida » Dom Out 14, 2012 21:31

Geometria
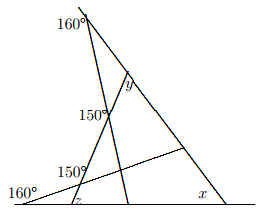
Os valores de 150º e 160º são indicados na figura a seguir.
aNEXO
Calcule o valor de 3x-2y+z:
(A) 180
(B) 190
(C) 200
(D) 210
Anexos
geometri.png
geometri.png (6.47 KiB) Exibido 1003 vezes
RafahAparecida
Novo Usuário
Novo Usuário
 
Mensagens: 7
Registrado em: Dom Out 14, 2012 20:46
Formação Escolar: ENSINO FUNDAMENTAL II
Andamento: cursando
Voltar ao topo

Re: Geometria

Mensagempor Vinicius_ » Seg Out 15, 2012 07:28

160° + 150º + z = 360º
z = 50º

160° + 150º + y = 360º
y = 50º

x + 50° + 50º = 180º
x = 80º

3x – 2y + z = 240º – 100º + 50º = 190º
Vinicius_
Novo Usuário
Novo Usuário
 
Mensagens: 5
Registrado em: Dom Out 14, 2012 14:50
Formação Escolar: ENSINO MÉDIO
Andamento: cursando
Voltar ao topo
Responder

Voltar para Geometria Plana

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 


Tópico Popular

Assunto: Exercicios de polinomios
Autor: shaft - Qua Jun 30, 2010 17:30

2x+5=\left(x+m\right)²-\left(x-n \right)²

Então, o exercicio pede para encontrar {m}^{3}-{n}^{3}.

Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !

Assunto: Exercicios de polinomios
Autor: Douglasm - Qua Jun 30, 2010 17:53

Bom, se desenvolvermos isso, encontramos:

2x+5 = 2x(m+n) + m^2-n^2

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):

2(m+n) = 2 \;\therefore\; m+n = 1

m^2-n^2 = 5 \;\therefore\; (m+n)(m-n) = 5 \;\therefore\; (m-n) = 5

Somando a primeira e a segunda equação:

2m = 6 \;\therefore\; m = 3 \;\mbox{consequentemente:}\; n=-2

Finalmente:

m^3 - n^3 = 27 + 8 = 35

Até a próxima.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum