o conjunto verdade da inequação 3/(x+1).(x-2)<0 é igual a:
-->é menor ou igual<--
eu esqueci o que é conjunto verdade e nao consegui resolver
tentei passar para o outro lada da inequaçaão multicando,mas e "x" desapareceria,pois ia multiplicar por 0.
o que devo fazer?
R:]-1,2[


 será positivo para
será positivo para  e negativo para
e negativo para 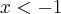 . Note pelas desigualdades
. Note pelas desigualdades 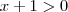 e
e  , assim
, assim  , segue que será positivo para
, segue que será positivo para  e negativo para
e negativo para  .
.![S = ]-1, 2[ S = ]-1, 2[](/latexrender/pictures/7e3d089bf88757ace372044fa0e9ed1a.png) .
.

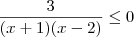
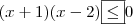 devemos fazer
devemos fazer 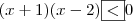 .
.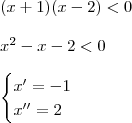
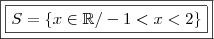 ou
ou ![\boxed{\boxed{S = ]- 1, 2[}} \boxed{\boxed{S = ]- 1, 2[}}](/latexrender/pictures/77fda918d97f485718d7ad2e54af14f6.png)


 .
.
 :
: