Na integra: "Exercicío: 7.24) Calcule a área do triângulo cujos vértices são os pontos A(2,1,-1), B(1,-1,0) e C(-1,1,2)". (Melo, Aline Resmine. Apostila de Álgebra Linear e Geometria Analítica, 2010, p.113).
- Para tento, pensei ná fórmula abaixo e resolvi:


Com o eixo 'Z', fica:


Resolução:

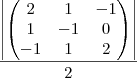

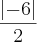


- No entanto, a resposta que consta no gabarito é:
![6\sqrt[]{2} 6\sqrt[]{2}](/latexrender/pictures/47873a0de37bfd7f9e4e44390bcce50f.png)
- E agora, senhor? Onde foi que eu errei? Oh God, why?
Abraços pessoal! Aguardando..


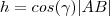
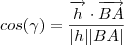
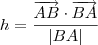 .Assim ,
.Assim , 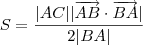 .
.

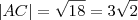
 .
.

 .
.
 :
: