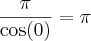por dileivas » Ter Out 09, 2012 19:30
por dileivas » Ter Out 09, 2012 19:30
O limite é o seguinte:

Pensei em multiplicar em cima e embaixo por pi*x pra tentar cair num limite fundamental, mas não bate com a resposta (que seria pi). Deve ser porque x não está tendendo a zero, não configurando um limite fundamental.
Alguém poderia me ajudar?
Obrigado!
-
dileivas
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Mar 14, 2012 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências e Tecnologia / Engenharia
- Andamento: cursando
 por dileivas » Sex Out 12, 2012 14:43
por dileivas » Sex Out 12, 2012 14:43
ninguém? =/
-
dileivas
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Mar 14, 2012 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências e Tecnologia / Engenharia
- Andamento: cursando
 por young_jedi » Sex Out 12, 2012 14:47
por young_jedi » Sex Out 12, 2012 14:47
Amigo não sei se voce ja estudou derivada e Teorema de L'hospital
esse limite ai pode ser resolvido por esse metodo, comente ai qualquer cosia
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por LuizAquino » Sex Out 12, 2012 15:32
por LuizAquino » Sex Out 12, 2012 15:32
dileivas escreveu:O limite é o seguinte:

Pensei em multiplicar em cima e embaixo por pi*x pra tentar cair num limite fundamental, mas não bate com a resposta (que seria pi). Deve ser porque x não está tendendo a zero, não configurando um limite fundamental.
Alguém poderia me ajudar?
young_jedi escreveu:Amigo não sei se voce ja estudou derivada e Teorema de L'hospital
esse limite ai pode ser resolvido por esse metodo, comente ai qualquer cosia
Para resolver esse exercício sem usar a Regra de L'Hospital, podemos proceder como indicado abaixo.
Fazendo a substituição de variáveis

, como temos
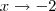
sabemos que
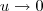
.
Ficamos então com:

Lembrando da definição de tangente, podemos ainda escrever que:

Aplicando então a identidade trigonométrica
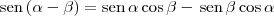
, temos que:

Agora tente concluir o exercício a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por dileivas » Sex Out 12, 2012 17:12
por dileivas » Sex Out 12, 2012 17:12
Meu resultado ainda está errado... teria que dar

. O que estou errando?

,
Tendo que

é um limite fundamental, que é igual a 1.
Como
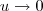
temos
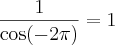
Não poderei aplicar o Teorema de L'hospital na prova 1 ainda, por isso tenho que resolver esse limite de outra forma...
Obrigado pela ajuda!
-
dileivas
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Mar 14, 2012 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências e Tecnologia / Engenharia
- Andamento: cursando
 por young_jedi » Sex Out 12, 2012 17:20
por young_jedi » Sex Out 12, 2012 17:20
voce multiplica e divide a equação por

, para chegar ao limite fundamental até ai esta certo,
mais em sua proxima passgem matematica voce "desaparece " com o

que esta em cima, acho que voce se esqueceu dele por isso o resultado não da certo.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por dileivas » Sex Out 12, 2012 17:33
por dileivas » Sex Out 12, 2012 17:33
Apesar de não saber o que errei na resposta anterior, consegui chegar no resultado de outra forma:

Se aplicarmos a identidade trigonométrica

, teremos

Como

é um limite fundamental, que é igual a 1, resta
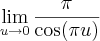
Como
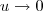
, temos
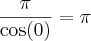
Está correto!?
Obrigado! =D
-
dileivas
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Mar 14, 2012 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências e Tecnologia / Engenharia
- Andamento: cursando
 por dileivas » Sex Out 12, 2012 17:36
por dileivas » Sex Out 12, 2012 17:36
young_jedi escreveu:voce multiplica e divide a equação por

, para chegar ao limite fundamental até ai esta certo,
mais em sua proxima passgem matematica voce "desaparece " com o

que esta em cima, acho que voce se esqueceu dele por isso o resultado não da certo.
Aaaah! Verdade! Só tinha esquecido do

! Daria certo também, foi falta de atenção...
Obrigado! Ajudaram muito!
-
dileivas
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Mar 14, 2012 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências e Tecnologia / Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- resolver problema funçao,não consigo montar,nem começar.
por [mariafernanda] » Qua Set 28, 2011 01:04
- 1 Respostas
- 2075 Exibições
- Última mensagem por Neperiano

Qua Set 28, 2011 15:18
Funções
-
- [Esperança] Não consigo começar o problema
por CBRJ » Qua Mar 06, 2013 23:52
- 0 Respostas
- 1246 Exibições
- Última mensagem por CBRJ

Qua Mar 06, 2013 23:52
Estatística
-
- Não sei como começar a resolver esse problema
por Sil » Ter Nov 02, 2010 19:36
- 5 Respostas
- 6256 Exibições
- Última mensagem por Sil

Ter Nov 02, 2010 21:40
Matemática Financeira
-
- [Funções] Questão a qual não sei por onde começar a resolver
por Richard Oliveira » Qua Nov 09, 2011 20:30
- 6 Respostas
- 3770 Exibições
- Última mensagem por Richard Oliveira

Qua Nov 09, 2011 23:17
Funções
-
- P.A nao consigo resolver essa p.a.
por Dalila » Sex Nov 14, 2008 16:58
- 2 Respostas
- 3131 Exibições
- Última mensagem por admin

Sex Nov 14, 2008 17:29
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 , como temos
, como temos 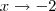 sabemos que
sabemos que 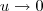 .
.

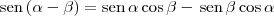 , temos que:
, temos que:

 . O que estou errando?
. O que estou errando? ,
, é um limite fundamental, que é igual a 1.
é um limite fundamental, que é igual a 1.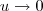 temos
temos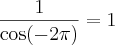

 , teremos
, teremos
 é um limite fundamental, que é igual a 1, resta
é um limite fundamental, que é igual a 1, resta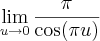
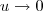 , temos
, temos