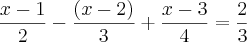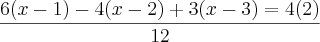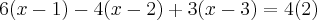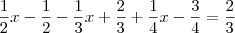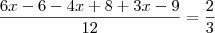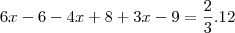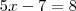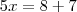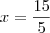por lais1906 » Qui Out 11, 2012 14:47
por lais1906 » Qui Out 11, 2012 14:47
qual a raiz da equação
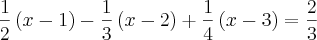
?
eu não sei nem por onde começar se tenho que fazer o mmc se tem que multiplicar me ajudem
-
lais1906
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qui Out 11, 2012 14:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ciencias contabeis
- Andamento: cursando
 por Cleyson007 » Qui Out 11, 2012 15:05
por Cleyson007 » Qui Out 11, 2012 15:05
Olá, boa tarde Lais.
Desejo-lhe as boas vindas!
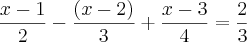
Tirando o MMC, temos:
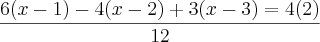
Eliminando o denominador 12, e trabalhando apenas com o numerador. Temos:
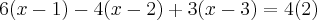
Consegue resolver sozinha a partir daqui?
Qualquer coisa estou por aqui

Att,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por lais1906 » Sáb Out 13, 2012 00:17
por lais1906 » Sáb Out 13, 2012 00:17
muito obrigado vocês são de mais ;]
-
lais1906
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qui Out 11, 2012 14:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ciencias contabeis
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Raíz de equação
por rafaela10g » Sex Ago 14, 2009 22:06
- 2 Respostas
- 7968 Exibições
- Última mensagem por Elcioschin

Sáb Ago 15, 2009 19:42
Sistemas de Equações
-
- equação simples com raiz
por Debylow » Ter Dez 04, 2012 15:18
- 3 Respostas
- 2285 Exibições
- Última mensagem por Cleyson007

Qua Dez 05, 2012 07:52
Equações
-
- FEI - Equação com Raíz Quadrada
por MMUNOZ » Sex Mai 10, 2013 12:22
- 0 Respostas
- 1096 Exibições
- Última mensagem por MMUNOZ

Sex Mai 10, 2013 12:22
Equações
-
- [raiz] equação epcar
por Ederson_ederson » Seg Jul 13, 2015 10:12
- 4 Respostas
- 3501 Exibições
- Última mensagem por Ederson_ederson

Qui Jul 16, 2015 16:56
Álgebra Elementar
-
- Equação raiz e polinomio
por Rosi7 » Sáb Mai 23, 2015 09:44
- 3 Respostas
- 2739 Exibições
- Última mensagem por Rosi7

Qui Mai 28, 2015 19:33
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
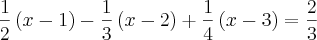 ?
?
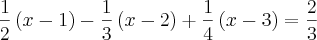 ?
?