Escreva as equações paramétricas do plano paralelo ao eixo z e que contém a interseção dos planos
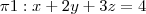e 
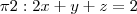.Gabarito:
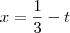
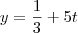
Eu o fiz, mas não tenho certeza se fiz corretamente pois não bateu com o gabarito. Por favor, analisem e vejam se meu raciocínio está correto.
A primeira coisa que fiz foi achar a interseção dos dois planos dados. Fiz o sistema por escalonamento, e achei este ponto
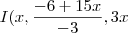). Sabe-se que a interseção de dois planos é uma reta, portanto este ponto I é um ponto pertencente desta reta. Atribuindo valores ao x do ponto I, temos:Atribuindo x=0,
encontramos este ponto da reta:
A(0,2,0)
Atribuindo x=1,
encontramos este ponto da reta:
B(1,-3,3)
Portanto, temos 2 pontos da reta e posso achar o vetor diretor
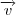, então temos 
.Para achar a equação paramétrica do plano, preciso de mais um vetor que não seja colinear a
. Somente com estes dados não sei achar mais um vetor não colinear ao vetor obtido.Então, decidi primeiro encontrar a equação geral do plano.
Primeiro, atribui mais um valor ao x de
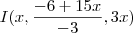para ter mais um ponto da reta (sei que não havia necessidade, pois eu poderia usar um dos pontos já obtidos, mas optei por faze-lo).Atribuindo x=2,
obtive C(2,-8,6).
Então, para obter a equação geral do plano, tenho este ponto C e sei que o plano é paralelo ao eixo z, ou seja, a variável z é livre.
Então temos:
, dividindo a equação por a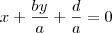
, colocando 
e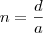 
temos:
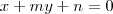, substituindo o ponto C(2,-8,6)
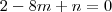, isolando o n
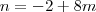, substituindo o valor de n em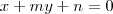 
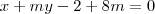, atribuindo um valor a variável m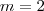
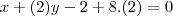
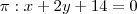
Portanto, encontrei a equação geral do plano a partir deste método que aprendi com o young_jedi daqui do ajudamatematica.com
Agora preciso achar mais um ponto qualquer pertencente a este plano e atribuindo valor ao x, temos
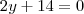
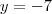,Então encontrei um ponto D(0,-7,0) pertencente ao plano.
Fazendo
, encontro um vetor não colinear ao 
Agora, tenho 2 vetores coplanares
e e não colineares e o ponto A(0,2,0).Então obtive que a equação paramétrica do plano é:
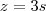
Estou certo? Obrigado
e