Olá cristina,
Começo por apresentar uma das possíveis maneiras de resolver a tua primeira inequação:

Primeiro achamos as raízes da equação:

factorizando, obtemos:

Logo: x = 0 ou x = 1 (Nota: Podemos também usar a fórmula resolvente se quisermos)
Em seguida construímos o quadro de sinais (I) (ver anexo 1):
Como podemos notar no quadro, a solução da inequação

é o intervalo:
![]-\infty,0[\cup]1,+\infty[ ]-\infty,0[\cup]1,+\infty[](/latexrender/pictures/cec5d89ffdd580d5ba482f8daaab75ea.png)
Olhando para o quadro acima apresentado, podemos ainda lembrar que a parábola de equação
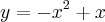
tem a concavidade voltada para baixo.
------------------------------------------------------------------------------------
Quanto à segunda inequação:
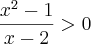
Achamos as raízes da equação:
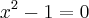
Factorizando, obtemos:
(x+1).(x-1)=0
Logo: x = -1 e x = 1
Em seguida, calculamos a raiz do denominador e obtemos: x -2 = 0 <=> x = 2
Podemos construir então o nosso quadro de sinais (II) (ver anexo 2):
Nota: s/s (sem significado)
Assim, a solução da inequação
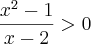
é o intervalo:
![]-1,1[\cup]2,+\infty[ ]-1,1[\cup]2,+\infty[](/latexrender/pictures/e26e07ea83eedd62898da252e7103b28.png)
Espero ter ajudado e aguardo a opinião de outros participantes!
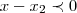 é o intervalo (0, 1]
é o intervalo (0, 1] é o intervalo (-1, 1)
é o intervalo (-1, 1) (2,infinito)
(2,infinito)
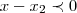 é o intervalo (0, 1]
é o intervalo (0, 1] é o intervalo (-1, 1)
é o intervalo (-1, 1) (2,infinito)
(2,infinito)



 é o intervalo:
é o intervalo: ![]-\infty,0[\cup]1,+\infty[ ]-\infty,0[\cup]1,+\infty[](/latexrender/pictures/cec5d89ffdd580d5ba482f8daaab75ea.png)
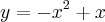 tem a concavidade voltada para baixo.
tem a concavidade voltada para baixo.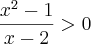
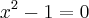
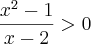 é o intervalo:
é o intervalo: ![]-1,1[\cup]2,+\infty[ ]-1,1[\cup]2,+\infty[](/latexrender/pictures/e26e07ea83eedd62898da252e7103b28.png)




 , avisa que eu resolvo.
, avisa que eu resolvo.

