 por womanizer » Seg Set 07, 2009 18:53
por womanizer » Seg Set 07, 2009 18:53
A figura:
http://i29.tinypic.com/wstjzp.jpg representa um quadrado com 10 cm de lado. Pede-se:
A) A área y da figura sombreada em função de x.
B) O valor de x para que essa área seja máxima.
C) A área máxima.Por favor, preciso disso
para amanhã bem cedo, me ajudem.

-
womanizer
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Set 07, 2009 18:44
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: estudante
- Andamento: cursando
 por Marcampucio » Seg Set 07, 2009 20:35
por Marcampucio » Seg Set 07, 2009 20:35

A área procurada é a soma das áreas dos dois trapézios indicados na figura:

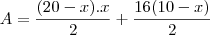
depois de mais algumas passagens chegamos a
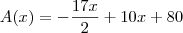
que é a função procurada e cujo valor máximo ocorre no vértice da parábola por ela representada
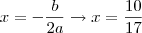
a área máxima é obtida substituindo o valor de x na função

A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda ai urgente...por favor...
por Jukilo » Seg Set 21, 2009 14:21
- 10 Respostas
- 5053 Exibições
- Última mensagem por Jukilo

Seg Set 21, 2009 23:50
Sistemas de Equações
-
- ajuda urgente por favor
por angela cardoso » Qua Ago 08, 2012 15:16
- 1 Respostas
- 1799 Exibições
- Última mensagem por e8group

Qua Ago 08, 2012 15:25
Equações
-
- POOR FAVOR AJUDA URGENTE
por felipinho » Sex Nov 21, 2008 19:47
- 4 Respostas
- 2919 Exibições
- Última mensagem por felipinho

Sáb Nov 22, 2008 17:15
Logaritmos
-
- preciso de ajuda urgente por favor
por weverton » Qua Jun 23, 2010 17:56
- 0 Respostas
- 1495 Exibições
- Última mensagem por weverton

Qua Jun 23, 2010 17:56
Matemática Financeira
-
- Por favor preciso de ajuda urgente!!!!
 por Queren » Seg Fev 06, 2012 21:09
por Queren » Seg Fev 06, 2012 21:09
- 1 Respostas
- 1937 Exibições
- Última mensagem por LuizAquino

Ter Fev 07, 2012 10:33
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






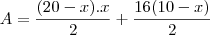
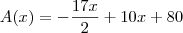 que é a função procurada e cujo valor máximo ocorre no vértice da parábola por ela representada
que é a função procurada e cujo valor máximo ocorre no vértice da parábola por ela representada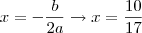




 , avisa que eu resolvo.
, avisa que eu resolvo.

