 por sindorf » Dom Set 06, 2009 20:42
por sindorf » Dom Set 06, 2009 20:42
Não tenho idéia de como resolver esta inequação:

-
sindorf
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Set 06, 2009 20:23
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso em informática
- Andamento: cursando
 por Marcampucio » Seg Set 07, 2009 00:04
por Marcampucio » Seg Set 07, 2009 00:04
sindorf escreveu:Não tenho idéia de como resolver esta inequação:

encontrando as raízes do trinomio do segundo grau escrevemos

para que o produto acima seja positivo devemos ter uma combinação de sinais
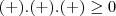
ou

o quadro abaixo faz o estudo dos sinais

vemos que o produto é positivo ou nulo para

e

visite:
http://pir2.forumeiros.com/forum.htm..
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Não consigo resolver esta questão.
por marianacarvalhops » Sex Mai 15, 2009 21:10
- 2 Respostas
- 2597 Exibições
- Última mensagem por admin

Sáb Mai 16, 2009 21:12
Trigonometria
-
- Não consigo resolver esta equação
por Ariel » Seg Nov 09, 2015 19:49
- 4 Respostas
- 3074 Exibições
- Última mensagem por eulercx

Ter Nov 10, 2015 10:52
Álgebra Elementar
-
- Não consigo resolver esta questão, por favor me ajudem!
por Derlan » Ter Jul 04, 2017 15:32
- 0 Respostas
- 1952 Exibições
- Última mensagem por Derlan

Ter Jul 04, 2017 15:32
Geometria Analítica
-
- [Equaçoes] me ajudem a resolver esta inequação
por teilom » Dom Ago 04, 2013 17:08
- 1 Respostas
- 2081 Exibições
- Última mensagem por DanielFerreira

Dom Ago 04, 2013 19:51
Equações
-
- inequação do 2 grau.resolver esta questao de prova
por adriano vieira » Ter Abr 22, 2014 22:21
- 0 Respostas
- 1367 Exibições
- Última mensagem por adriano vieira

Ter Abr 22, 2014 22:21
Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






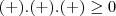 ou
ou 

 e
e 


 .
.
 :
: