 por samra » Sáb Out 06, 2012 15:41
por samra » Sáb Out 06, 2012 15:41
Como faço para provar a identidade hiperbólica abaixo?
![senh\left(\frac{1}{2}x \right) = +- \sqrt[]{\frac{cosh x-1}{2}} senh\left(\frac{1}{2}x \right) = +- \sqrt[]{\frac{cosh x-1}{2}}](/latexrender/pictures/b6c2ce823bd1503f71dc87bd2af9ecac.png)
Obg
"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
 por MarceloFantini » Sáb Out 06, 2012 16:16
por MarceloFantini » Sáb Out 06, 2012 16:16
Você pode tentar usar a definição de seno hiperbólico:

, daí

e trabalhe pra chegar no quadrado da expressão dada.
Outra forma é você usar fórmulas de arco duplo de seno e cosseno hiperbólico (que eu não sei de cabeça), deve sair mais facilmente.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por samra » Sáb Out 06, 2012 18:02
por samra » Sáb Out 06, 2012 18:02
Olha o que eu fiz:
![senh \left(\frac{1}{2}x \right) = +- \sqrt[]{\frac{coshx-1}{2}}
=
cosh (x) = cosh \left(\frac{x}{2} + \frac{x}{2} \right)
=
cosh \left(\frac{x}{2} \right). cosh \left(\frac{x}{2} \right) + senh \left(\frac{x}{2} \right). senh \left(\frac{x}{2} \right)
=
{cosh}^{2}\left(\frac{x}{2} \right) + {senh}^{2}\left(\frac{x}{2} \right) senh \left(\frac{1}{2}x \right) = +- \sqrt[]{\frac{coshx-1}{2}}
=
cosh (x) = cosh \left(\frac{x}{2} + \frac{x}{2} \right)
=
cosh \left(\frac{x}{2} \right). cosh \left(\frac{x}{2} \right) + senh \left(\frac{x}{2} \right). senh \left(\frac{x}{2} \right)
=
{cosh}^{2}\left(\frac{x}{2} \right) + {senh}^{2}\left(\frac{x}{2} \right)](/latexrender/pictures/da0608212aee3ab69c802b8b30462fcc.png)
sendo

temos que:
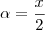
O que nos dá
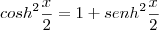
O que eu devo fazer agora?
Obg, att.
"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Demonstrar que a função f é igual a uma certa série
por fff » Seg Jan 05, 2015 17:15
- 4 Respostas
- 4626 Exibições
- Última mensagem por fff

Qua Jan 07, 2015 18:14
Sequências
-
- Conceitos de Trigonometria Esferica e Hiperbólica
por pequena » Dom Set 06, 2009 16:39
- 0 Respostas
- 1359 Exibições
- Última mensagem por pequena

Dom Set 06, 2009 16:39
Trigonometria
-
- Como demonstrar??
por manuoliveira » Sex Mar 23, 2012 18:25
- 2 Respostas
- 1514 Exibições
- Última mensagem por manuoliveira

Sáb Abr 14, 2012 19:33
Funções
-
- Demonstrar - Primitivas
por samra » Qua Out 03, 2012 23:54
- 3 Respostas
- 1944 Exibições
- Última mensagem por young_jedi

Sex Out 05, 2012 11:24
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade triangular] Demonstrar por absurdo
por Aliocha Karamazov » Qua Set 28, 2011 01:07
- 1 Respostas
- 1751 Exibições
- Última mensagem por LuizAquino

Qua Set 28, 2011 17:57
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![senh\left(\frac{1}{2}x \right) = +- \sqrt[]{\frac{cosh x-1}{2}} senh\left(\frac{1}{2}x \right) = +- \sqrt[]{\frac{cosh x-1}{2}}](/latexrender/pictures/b6c2ce823bd1503f71dc87bd2af9ecac.png)

![senh\left(\frac{1}{2}x \right) = +- \sqrt[]{\frac{cosh x-1}{2}} senh\left(\frac{1}{2}x \right) = +- \sqrt[]{\frac{cosh x-1}{2}}](/latexrender/pictures/b6c2ce823bd1503f71dc87bd2af9ecac.png)

 , daí
, daí  e trabalhe pra chegar no quadrado da expressão dada.
e trabalhe pra chegar no quadrado da expressão dada.

![senh \left(\frac{1}{2}x \right) = +- \sqrt[]{\frac{coshx-1}{2}}
=
cosh (x) = cosh \left(\frac{x}{2} + \frac{x}{2} \right)
=
cosh \left(\frac{x}{2} \right). cosh \left(\frac{x}{2} \right) + senh \left(\frac{x}{2} \right). senh \left(\frac{x}{2} \right)
=
{cosh}^{2}\left(\frac{x}{2} \right) + {senh}^{2}\left(\frac{x}{2} \right) senh \left(\frac{1}{2}x \right) = +- \sqrt[]{\frac{coshx-1}{2}}
=
cosh (x) = cosh \left(\frac{x}{2} + \frac{x}{2} \right)
=
cosh \left(\frac{x}{2} \right). cosh \left(\frac{x}{2} \right) + senh \left(\frac{x}{2} \right). senh \left(\frac{x}{2} \right)
=
{cosh}^{2}\left(\frac{x}{2} \right) + {senh}^{2}\left(\frac{x}{2} \right)](/latexrender/pictures/da0608212aee3ab69c802b8b30462fcc.png)
 temos que:
temos que: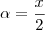
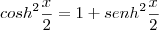


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.