 por funtastic_lif » Sáb Out 06, 2012 09:30
por funtastic_lif » Sáb Out 06, 2012 09:30
Bom dia,
Tenho-me debatido com o seguinte problema

Uploaded with
ImageShack.usO resultado que me dá não está igual às soluções do livro.
A Minha Resolução:


![Tg\alpha=\frac{Cos\alpha}{Sen\alpha}=\frac{5}{3}] Tg\alpha=\frac{Cos\alpha}{Sen\alpha}=\frac{5}{3}]](/latexrender/pictures/063297ddedfb5a68d3833d23b675302f.png)
Nas Soluções:

-
funtastic_lif
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Out 06, 2012 08:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Sáb Out 06, 2012 14:09
por young_jedi » Sáb Out 06, 2012 14:09
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por funtastic_lif » Sáb Out 06, 2012 14:14
por funtastic_lif » Sáb Out 06, 2012 14:14
Obrigado.
Distração minha.
-
funtastic_lif
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Out 06, 2012 08:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Trigonometria) problema trigonometria
por Luizap11 » Qui Dez 05, 2013 00:33
- 2 Respostas
- 5258 Exibições
- Última mensagem por Edunclec

Qui Dez 05, 2013 20:53
Trigonometria
-
- Problema de Trigonometria
por Dimas » Ter Nov 09, 2010 11:32
- 7 Respostas
- 5740 Exibições
- Última mensagem por Molina

Qui Jul 14, 2011 20:34
Trigonometria
-
- Trigonometria - Problema
 por RodriguesBruno » Qui Mai 22, 2014 18:26
por RodriguesBruno » Qui Mai 22, 2014 18:26
- 2 Respostas
- 2071 Exibições
- Última mensagem por RodriguesBruno

Sex Mai 23, 2014 15:30
Trigonometria
-
- Problema Trigonometria
por marinalcd » Dom Jun 11, 2017 16:58
- 0 Respostas
- 3223 Exibições
- Última mensagem por marinalcd

Dom Jun 11, 2017 16:58
Trigonometria
-
- Ajudem !! Trigonometria - problema ...
 por Lunn » Qua Mar 09, 2011 15:58
por Lunn » Qua Mar 09, 2011 15:58
- 2 Respostas
- 2237 Exibições
- Última mensagem por Lunn

Qua Mar 09, 2011 19:50
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![Tg\alpha=\frac{Cos\alpha}{Sen\alpha}=\frac{5}{3}] Tg\alpha=\frac{Cos\alpha}{Sen\alpha}=\frac{5}{3}]](/latexrender/pictures/063297ddedfb5a68d3833d23b675302f.png)





![Tg\alpha=\frac{Cos\alpha}{Sen\alpha}=\frac{5}{3}] Tg\alpha=\frac{Cos\alpha}{Sen\alpha}=\frac{5}{3}]](/latexrender/pictures/063297ddedfb5a68d3833d23b675302f.png)



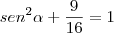
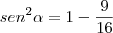


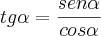



 .
.
 :
: