 por fabriel » Sex Out 05, 2012 02:47
por fabriel » Sex Out 05, 2012 02:47
E ai Pessoal empaquei em uma aqui. É dada a Integral:
![\int_{}^{}\frac{dx}{\sqrt[]{1+\sqrt[3]{x}}} \int_{}^{}\frac{dx}{\sqrt[]{1+\sqrt[3]{x}}}](/latexrender/pictures/30511c93c2a14b9c61e0048ba0601936.png)
Então devo chamar:
![u=\sqrt[3]{x} u=\sqrt[3]{x}](/latexrender/pictures/dd75434167bc7231f965d49667e1c4ea.png)
então:
![du=\frac{1}{3\sqrt[3]{{x}^{2}}}dx du=\frac{1}{3\sqrt[3]{{x}^{2}}}dx](/latexrender/pictures/aa3f983faf31910d2b87675bb21eb6e1.png)
só q fica complicado na hora da substituição
Então esta certo esse caminho?
ou devo fazer outro tipo de substituição??
obrigado!!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por LuizAquino » Sex Out 05, 2012 09:57
por LuizAquino » Sex Out 05, 2012 09:57
fabriel escreveu:E ai Pessoal empaquei em uma aqui. É dada a Integral:
![\int_{}^{}\frac{dx}{\sqrt[]{1+\sqrt[3]{x}}} \int_{}^{}\frac{dx}{\sqrt[]{1+\sqrt[3]{x}}}](/latexrender/pictures/30511c93c2a14b9c61e0048ba0601936.png)
Então devo chamar:
![u=\sqrt[3]{x} u=\sqrt[3]{x}](/latexrender/pictures/dd75434167bc7231f965d49667e1c4ea.png)
então:
![du=\frac{1}{3\sqrt[3]{{x}^{2}}}dx du=\frac{1}{3\sqrt[3]{{x}^{2}}}dx](/latexrender/pictures/aa3f983faf31910d2b87675bb21eb6e1.png)
só q fica complicado na hora da substituição
Então esta certo esse caminho?
ou devo fazer outro tipo de substituição??
Use a substituição
![u = 1 + \sqrt[3]{x} u = 1 + \sqrt[3]{x}](/latexrender/pictures/d2064e3d1d0200fecff8ac86521f61af.png)
e
![du = \frac{1}{3\sqrt[3]{x^2}}\,dx du = \frac{1}{3\sqrt[3]{x^2}}\,dx](/latexrender/pictures/517fdbae39ce2626a2c64d7d8aaedb2a.png)
.
Como você usou
![u=1 + \sqrt[3]{x} u=1 + \sqrt[3]{x}](/latexrender/pictures/0cc91a530cb4e2c28072b7439bba868e.png)
, então você pode dizer que
![(u - 1)^2 = \sqrt[3]{x^2} (u - 1)^2 = \sqrt[3]{x^2}](/latexrender/pictures/f3cb7610fded051d96e68cf7e4f29194.png)
. Desse modo, você pode escrever que
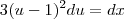
.
Portanto, você terá que:
![\int\frac{1}{\sqrt{1+\sqrt[3]{x}}}\,dx = \int\frac{3(u - 1)^2}{\sqrt{u}}\,du \int\frac{1}{\sqrt{1+\sqrt[3]{x}}}\,dx = \int\frac{3(u - 1)^2}{\sqrt{u}}\,du](/latexrender/pictures/9a645fd8577c56971c0897a1ab150b01.png)
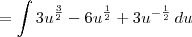
Agora tente prosseguir a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fabriel » Sex Out 05, 2012 13:20
por fabriel » Sex Out 05, 2012 13:20
Obrigado Luiz, calculei aqui:
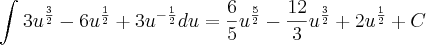
desse tipo que está ai eu posso simplifica o resultado? Se não fica por isso mesmo:
![\frac{6}{5}\sqrt[]{1+{\sqrt[3]{x}}^{5}}-\frac{12}{3}\sqrt[]{1+{\sqrt[3]{x}}^{3}}+2\sqrt[]{1+\sqrt[3]{x}}+C \frac{6}{5}\sqrt[]{1+{\sqrt[3]{x}}^{5}}-\frac{12}{3}\sqrt[]{1+{\sqrt[3]{x}}^{3}}+2\sqrt[]{1+\sqrt[3]{x}}+C](/latexrender/pictures/0f47a64036b7d9b3190bc4a0beb874e0.png)
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por LuizAquino » Sex Out 05, 2012 15:23
por LuizAquino » Sex Out 05, 2012 15:23
fabriel escreveu:Obrigado Luiz, calculei aqui:
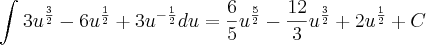
Errado. O correto seria:
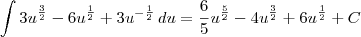
fabriel escreveu:desse tipo que está ai eu posso simplifica o resultado?
Não dá para simplificar muita coisa.
fabriel escreveu:Se não fica por isso mesmo:
![\frac{6}{5}\sqrt[]{1+{\sqrt[3]{x}}^{5}}-\frac{12}{3}\sqrt[]{1+{\sqrt[3]{x}}^{3}}+2\sqrt[]{1+\sqrt[3]{x}}+C \frac{6}{5}\sqrt[]{1+{\sqrt[3]{x}}^{5}}-\frac{12}{3}\sqrt[]{1+{\sqrt[3]{x}}^{3}}+2\sqrt[]{1+\sqrt[3]{x}}+C](/latexrender/pictures/0f47a64036b7d9b3190bc4a0beb874e0.png)
Errado. O correto seria:
![\frac{6}{5}\sqrt{\left(1+\sqrt[3]{x}\right)^5} - 4\sqrt{\left(1+\sqrt[3]{x}\right)^3} + 6\sqrt{1+\sqrt[3]{x}} + C \frac{6}{5}\sqrt{\left(1+\sqrt[3]{x}\right)^5} - 4\sqrt{\left(1+\sqrt[3]{x}\right)^3} + 6\sqrt{1+\sqrt[3]{x}} + C](/latexrender/pictures/2942f176ce43428472ae3e699a292e65.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fabriel » Sex Out 05, 2012 17:22
por fabriel » Sex Out 05, 2012 17:22
ha sim errei nesse detalhe, agora q fui ver:
![3\int_{}^{}{u}^{-\frac{1}{2}}du=3\left[{2u}^{\frac{1}{2}}+C1 \right]=6{u}^{\frac{1}{2}}+C1 3\int_{}^{}{u}^{-\frac{1}{2}}du=3\left[{2u}^{\frac{1}{2}}+C1 \right]=6{u}^{\frac{1}{2}}+C1](/latexrender/pictures/8e9dbda58a93121adb0e312515eed9ad.png)
obrigado de novo!
Tenha um Bom fim de semana!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [integral indefinida] qual o processo de resolução a usar
por armando » Seg Jul 29, 2013 23:53
- 11 Respostas
- 6304 Exibições
- Última mensagem por Man Utd

Ter Jul 30, 2013 20:09
Cálculo: Limites, Derivadas e Integrais
-
- qual é a integral indefinida passo-a-passo de:
por Raphison » Seg Dez 01, 2014 10:53
- 2 Respostas
- 1618 Exibições
- Última mensagem por Raphison

Qua Dez 03, 2014 08:42
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
por gdarius » Ter Mar 16, 2010 15:57
- 5 Respostas
- 5625 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 31, 2012 19:32
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
 por CrazzyVi » Ter Ago 17, 2010 21:41
por CrazzyVi » Ter Ago 17, 2010 21:41
- 1 Respostas
- 2708 Exibições
- Última mensagem por Lucio Carvalho

Qua Ago 18, 2010 08:27
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
por felipealves » Ter Jun 21, 2011 11:48
- 3 Respostas
- 3984 Exibições
- Última mensagem por felipealves

Ter Jun 21, 2011 20:59
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\frac{dx}{\sqrt[]{1+\sqrt[3]{x}}} \int_{}^{}\frac{dx}{\sqrt[]{1+\sqrt[3]{x}}}](/latexrender/pictures/30511c93c2a14b9c61e0048ba0601936.png)
![u=\sqrt[3]{x} u=\sqrt[3]{x}](/latexrender/pictures/dd75434167bc7231f965d49667e1c4ea.png)
![du=\frac{1}{3\sqrt[3]{{x}^{2}}}dx du=\frac{1}{3\sqrt[3]{{x}^{2}}}dx](/latexrender/pictures/aa3f983faf31910d2b87675bb21eb6e1.png)

![\int_{}^{}\frac{dx}{\sqrt[]{1+\sqrt[3]{x}}} \int_{}^{}\frac{dx}{\sqrt[]{1+\sqrt[3]{x}}}](/latexrender/pictures/30511c93c2a14b9c61e0048ba0601936.png)
![u=\sqrt[3]{x} u=\sqrt[3]{x}](/latexrender/pictures/dd75434167bc7231f965d49667e1c4ea.png)
![du=\frac{1}{3\sqrt[3]{{x}^{2}}}dx du=\frac{1}{3\sqrt[3]{{x}^{2}}}dx](/latexrender/pictures/aa3f983faf31910d2b87675bb21eb6e1.png)

![u = 1 + \sqrt[3]{x} u = 1 + \sqrt[3]{x}](/latexrender/pictures/d2064e3d1d0200fecff8ac86521f61af.png) e
e ![du = \frac{1}{3\sqrt[3]{x^2}}\,dx du = \frac{1}{3\sqrt[3]{x^2}}\,dx](/latexrender/pictures/517fdbae39ce2626a2c64d7d8aaedb2a.png) .
.![u=1 + \sqrt[3]{x} u=1 + \sqrt[3]{x}](/latexrender/pictures/0cc91a530cb4e2c28072b7439bba868e.png) , então você pode dizer que
, então você pode dizer que ![(u - 1)^2 = \sqrt[3]{x^2} (u - 1)^2 = \sqrt[3]{x^2}](/latexrender/pictures/f3cb7610fded051d96e68cf7e4f29194.png) . Desse modo, você pode escrever que
. Desse modo, você pode escrever que 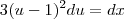 .
.![\int\frac{1}{\sqrt{1+\sqrt[3]{x}}}\,dx = \int\frac{3(u - 1)^2}{\sqrt{u}}\,du \int\frac{1}{\sqrt{1+\sqrt[3]{x}}}\,dx = \int\frac{3(u - 1)^2}{\sqrt{u}}\,du](/latexrender/pictures/9a645fd8577c56971c0897a1ab150b01.png)
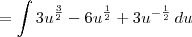

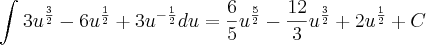
![\frac{6}{5}\sqrt[]{1+{\sqrt[3]{x}}^{5}}-\frac{12}{3}\sqrt[]{1+{\sqrt[3]{x}}^{3}}+2\sqrt[]{1+\sqrt[3]{x}}+C \frac{6}{5}\sqrt[]{1+{\sqrt[3]{x}}^{5}}-\frac{12}{3}\sqrt[]{1+{\sqrt[3]{x}}^{3}}+2\sqrt[]{1+\sqrt[3]{x}}+C](/latexrender/pictures/0f47a64036b7d9b3190bc4a0beb874e0.png)

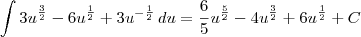
![\frac{6}{5}\sqrt{\left(1+\sqrt[3]{x}\right)^5} - 4\sqrt{\left(1+\sqrt[3]{x}\right)^3} + 6\sqrt{1+\sqrt[3]{x}} + C \frac{6}{5}\sqrt{\left(1+\sqrt[3]{x}\right)^5} - 4\sqrt{\left(1+\sqrt[3]{x}\right)^3} + 6\sqrt{1+\sqrt[3]{x}} + C](/latexrender/pictures/2942f176ce43428472ae3e699a292e65.png)

![3\int_{}^{}{u}^{-\frac{1}{2}}du=3\left[{2u}^{\frac{1}{2}}+C1 \right]=6{u}^{\frac{1}{2}}+C1 3\int_{}^{}{u}^{-\frac{1}{2}}du=3\left[{2u}^{\frac{1}{2}}+C1 \right]=6{u}^{\frac{1}{2}}+C1](/latexrender/pictures/8e9dbda58a93121adb0e312515eed9ad.png)

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)