 por Russman » Qui Out 04, 2012 21:24
por Russman » Qui Out 04, 2012 21:24
Eu preciso de ajuda na seguinte questão:
Represente a função
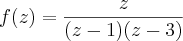
por meio de uma série de potências positivas e negativas de

que convirja para

quando

.
Eu sei que como a função possui pontos singulares existirão termos da sequencia de Taylor de Laurent. Mas eu não sei em torno de qual ponto eu devo fazer a expansão. Eu imagino que devo fazer em torno de

. Mas esse ponto dá problema na derivada

-ésima de

. E no mais a função possui 2 pontos singulares. Não sei como proceder.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por young_jedi » Qui Out 04, 2012 22:06
por young_jedi » Qui Out 04, 2012 22:06

um termo da serie é

ai pros outros termos voce aplica a derivada pra achar a serie de potencias de
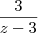
a serie é em torno do ponto 1 mesmo.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Russman » Qui Out 04, 2012 22:20
por Russman » Qui Out 04, 2012 22:20
Valeeu amigo! Consegui.

"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Série de Potências Complexos [2]
por Russman » Qui Out 04, 2012 23:21
- 1 Respostas
- 1983 Exibições
- Última mensagem por young_jedi

Sex Out 05, 2012 11:39
Números Complexos
-
- Construir uma serie de potencias
por Sofia fonseca » Ter Mar 05, 2013 16:23
- 0 Respostas
- 2254 Exibições
- Última mensagem por Sofia fonseca

Ter Mar 05, 2013 16:23
Sequências
-
- Números Complexos, Potências.
por FrIcaro » Seg Ago 10, 2009 16:11
- 2 Respostas
- 2608 Exibições
- Última mensagem por Elcioschin

Sáb Ago 15, 2009 20:33
Números Complexos
-
- SERIE CONVERGENTE DE NUMEROS COMPLEXOS
 por Jadiel Carlos » Sex Jan 19, 2018 02:35
por Jadiel Carlos » Sex Jan 19, 2018 02:35
- 0 Respostas
- 4631 Exibições
- Última mensagem por Jadiel Carlos

Sex Jan 19, 2018 02:35
Números Complexos
-
- [Série] Calcular valor de série tendo outra como referência
por robmenas » Dom Abr 07, 2019 14:35
- 0 Respostas
- 9180 Exibições
- Última mensagem por robmenas

Dom Abr 07, 2019 14:35
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
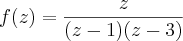
 que convirja para
que convirja para  quando
quando  .
. . Mas esse ponto dá problema na derivada
. Mas esse ponto dá problema na derivada  -ésima de
-ésima de  . E no mais a função possui 2 pontos singulares. Não sei como proceder.
. E no mais a função possui 2 pontos singulares. Não sei como proceder.



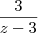

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.