 por samra » Qua Out 03, 2012 23:54
por samra » Qua Out 03, 2012 23:54
Um objeto é lançado para cima com velocidade inicial v
0 metros por segundo
a partir de um ponto s
0 metros acima do solo . Mostre que:
![{[v(t)]}^{2} {[v(t)]}^{2}](/latexrender/pictures/4d2e134a2e343142d6582712ca8f1d10.png) =
= 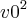 -
- 19,6[s(t)-s
0]
Resolver utilizando primitivas
Help me, please
att.Sammy
"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
 por young_jedi » Qui Out 04, 2012 11:22
por young_jedi » Qui Out 04, 2012 11:22
temos que

onde v(t) é a velocidade no tempo t e a é a acelereção
podemos escrever esta derivado como
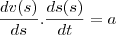
onde s(t) é a posição do objeto
mais

, então podemos dizer que
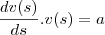
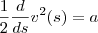
integrando ambos os lados da equação com relação a s


levando em conta que a=-9,8 aceleração da gravidade se chega na expressão
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por samra » Qui Out 04, 2012 22:23
por samra » Qui Out 04, 2012 22:23

Nessa linha vc aplicou a primitiva? Se sim porq o d/ds continua aparecendo?

Não intendi a parte abaixo:
integrando ambos os lados da equação com relação a s


levando em conta que a=-9,8 aceleração da gravidade se chega na expressão
Mto Obg!

"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
 por young_jedi » Sex Out 05, 2012 11:24
por young_jedi » Sex Out 05, 2012 11:24

isso é a derivada de
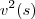
com relação a s
que pela regra da cadeia resulta em
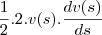
que é exatemaent oque tinhamos na equação anterior

na outra parte eu fiz a integral
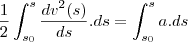
na primeira parte temos que a integral da derivada é a propria funçao
ou seja
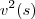
, para s variando de

ate um outro s qualquer
e na outra integral temos a integral de uma constante, que é igual propria constante vezes s, com s variando de

ate um s qualquer.

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como demonstrar??
por manuoliveira » Sex Mar 23, 2012 18:25
- 2 Respostas
- 1506 Exibições
- Última mensagem por manuoliveira

Sáb Abr 14, 2012 19:33
Funções
-
- Demonstrar função hiperbólica
por samra » Sáb Out 06, 2012 15:41
- 3 Respostas
- 2618 Exibições
- Última mensagem por MarceloFantini

Sáb Out 06, 2012 18:15
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade triangular] Demonstrar por absurdo
por Aliocha Karamazov » Qua Set 28, 2011 01:07
- 1 Respostas
- 1746 Exibições
- Última mensagem por LuizAquino

Qua Set 28, 2011 17:57
Álgebra Elementar
-
- Demonstrar que a função f é igual a uma certa série
por fff » Seg Jan 05, 2015 17:15
- 4 Respostas
- 4619 Exibições
- Última mensagem por fff

Qua Jan 07, 2015 18:14
Sequências
-
- [Teorema do Valor Médio] Demonstrar desigualdade
por Brunorp » Qua Abr 06, 2016 23:07
- 1 Respostas
- 1368 Exibições
- Última mensagem por adauto martins

Sex Abr 08, 2016 11:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{[v(t)]}^{2} {[v(t)]}^{2}](/latexrender/pictures/4d2e134a2e343142d6582712ca8f1d10.png) =
= 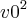 - 19,6[s(t)-s0]
- 19,6[s(t)-s0]
![{[v(t)]}^{2} {[v(t)]}^{2}](/latexrender/pictures/4d2e134a2e343142d6582712ca8f1d10.png) =
= 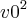 - 19,6[s(t)-s0]
- 19,6[s(t)-s0]

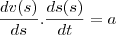
 , então podemos dizer que
, então podemos dizer que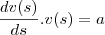
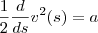



 Nessa linha vc aplicou a primitiva? Se sim porq o d/ds continua aparecendo?
Nessa linha vc aplicou a primitiva? Se sim porq o d/ds continua aparecendo? Não intendi a parte abaixo:
Não intendi a parte abaixo:


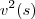 com relação a s
com relação a s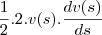

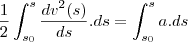
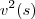 , para s variando de
, para s variando de  ate um outro s qualquer
ate um outro s qualquer ate um s qualquer.
ate um s qualquer.
