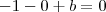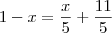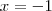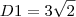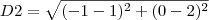por flaaacs » Qua Out 03, 2012 16:02
por flaaacs » Qua Out 03, 2012 16:02
Sejam r a reta de equacao y+x-1=0, s a reta que intercepta o eixo das coordenadas no ponto de ordenada y=-1 com r perpendicular a s e t a reta de equacao x-5y + 11=0. A area do triangulo delimitado pelas retas r,s e t é:
Resposta oficial: 6
-
flaaacs
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Out 03, 2012 15:58
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por young_jedi » Qua Out 03, 2012 16:16
por young_jedi » Qua Out 03, 2012 16:16
se as retas r e s são perpendiculares então elas formam um angulo de 90º sendo assim, é um triangulo retangulo onde o angulo reto esta na intersecção das retas r e s, calculando a intersecção da reta t com as retas s e r, tem se os outros dois pontos que formam o triangulo, calculando a distancias destes dois pontos ate o angulo de 90º tem se a medida dos catetos e com isso da pra calcular a area do triangulo
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por flaaacs » Qua Out 03, 2012 16:53
por flaaacs » Qua Out 03, 2012 16:53
Tentei achar as intersecções. Encontrei três pontos, mas acho que fiz errado. Encontrei r e s (2,-1) / s e t (-16,-1) / r e t (-1,2). Porém, fazendo os cálculos não acho a área correta. Acredito tbm que estou tendo dificuldade de visualizar o triângulo. Tem a possibilidade de efetuar os cálculos e talvez incluir o desenho, por favor?
-
flaaacs
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Out 03, 2012 15:58
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por young_jedi » Qua Out 03, 2012 17:25
por young_jedi » Qua Out 03, 2012 17:25
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Área limitada pelas curvas
por Fernandobertolaccini » Qua Jul 23, 2014 22:02
- 0 Respostas
- 1128 Exibições
- Última mensagem por Fernandobertolaccini

Qua Jul 23, 2014 22:02
Cálculo: Limites, Derivadas e Integrais
-
- Área limitada pelas curvas
por Fernandobertolaccini » Qua Jul 23, 2014 22:04
- 1 Respostas
- 1509 Exibições
- Última mensagem por matmatco

Sáb Ago 09, 2014 12:15
Cálculo: Limites, Derivadas e Integrais
-
- Qual a razão da PG formada pelas medidas do triângulo
 por andersontricordiano » Sex Mar 04, 2011 23:43
por andersontricordiano » Sex Mar 04, 2011 23:43
- 4 Respostas
- 3385 Exibições
- Última mensagem por Renato_RJ

Seg Mar 07, 2011 19:36
Progressões
-
- [Razão da área do triângulo para a área do quadrilátero]
 por Mayra Luna » Sex Nov 23, 2012 20:17
por Mayra Luna » Sex Nov 23, 2012 20:17
- 2 Respostas
- 4412 Exibições
- Última mensagem por Mayra Luna

Ter Nov 27, 2012 14:53
Geometria Plana
-
- Retas formando triângulo
por Aline Bianca » Ter Ago 24, 2010 22:20
- 2 Respostas
- 1600 Exibições
- Última mensagem por Aline Bianca

Qua Ago 25, 2010 21:36
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.