 por fabriel » Qua Out 03, 2012 16:20
por fabriel » Qua Out 03, 2012 16:20
Bom amigos, surgiu ma dúvida aqui quando estava integrando essa integral:

E eu estava reescrevendo na forma:
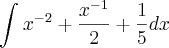
Mas não tenho certeza se isso esta certo, se eu posso escreve-la assim, pois:
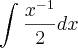
Vai dar uma indeterminação do tipo 1/0, então pesso ajuda nisso ai...É o caminho certo, ou devo usar outros métodos, se devo usar então de que jeito??
obrigado!!

Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por young_jedi » Qua Out 03, 2012 16:34
por young_jedi » Qua Out 03, 2012 16:34
voce não pode escrever da forma como colocou:
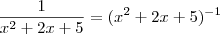
isto é diferente do que voce colocou, voce não pode distribuir os expoentes na soma de termos
uma forma melhor de resolver seria
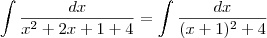
subsitituindo
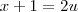
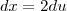
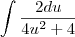

para esta ultima integral existe na tabela de integrais e esta relacionado ao arctang
é so pesquisar
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por MarceloFantini » Qua Out 03, 2012 16:34
por MarceloFantini » Qua Out 03, 2012 16:34
Você está cometendo um erro grave, note que

. Tome

para ver, a primeira expressão resulta em

enquanto que a outra nem está definida.
Assim como no outro tópico, escreva

e faça a substituição
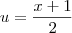
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fabriel » Qua Out 03, 2012 17:39
por fabriel » Qua Out 03, 2012 17:39
Valeu muito obrigado, por mostrar o caminho.
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integração por Partes] Integral indefinida...
por luiz_henriquear » Qui Dez 22, 2011 17:40
- 1 Respostas
- 3705 Exibições
- Última mensagem por LuizAquino

Qui Dez 22, 2011 21:58
Cálculo: Limites, Derivadas e Integrais
-
- [Integração por Partes] Integral indefinida...
por luiz_henriquear » Sáb Dez 31, 2011 14:35
- 2 Respostas
- 1964 Exibições
- Última mensagem por luiz_henriquear

Sáb Dez 31, 2011 15:08
Cálculo: Limites, Derivadas e Integrais
-
- Duvida Integral Indefinida
por cardoed001 » Sáb Fev 22, 2014 16:55
- 5 Respostas
- 4351 Exibições
- Última mensagem por Man Utd

Dom Fev 23, 2014 11:51
Cálculo: Limites, Derivadas e Integrais
-
- [integral indefinida] - dúvida
 por natanaelskt » Sáb Jun 28, 2014 09:25
por natanaelskt » Sáb Jun 28, 2014 09:25
- 3 Respostas
- 2610 Exibições
- Última mensagem por e8group

Sáb Jun 28, 2014 17:16
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL INDEFINIDA] Duvida no resultado
por fabriel » Sex Nov 02, 2012 13:57
- 1 Respostas
- 1505 Exibições
- Última mensagem por fraol

Seg Nov 19, 2012 22:00
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

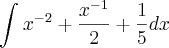
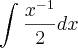



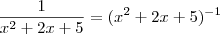
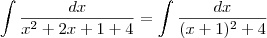
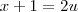
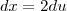
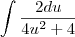


 . Tome
. Tome  para ver, a primeira expressão resulta em
para ver, a primeira expressão resulta em  enquanto que a outra nem está definida.
enquanto que a outra nem está definida. e faça a substituição
e faça a substituição 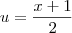 .
.


 .
.



