 . Prove que:
. Prove que: (a) Um ponto X pertence a reta determinada por A e B, se, e somente se,
CX (CX é um vetor, mas eu não achei a ''setinha'' no latex.) =
 CA (CA também é um vetor.) +
CA (CA também é um vetor.) +  CB, (CB é um vetor.) com \
CB, (CB é um vetor.) com \  +
+  = 1.
= 1. (b) Um ponto X pertence ao segmento AB se, e somente se,
CX (CX é vetor) =
 CA (CA vetor) +
CA (CA vetor) +  CB (CB é um vetor), com
CB (CB é um vetor), com 
 0,
0, 
 e
e  +
+  = 1
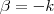
= 1(c) Um ponto X é um ponto interior ao triângulo ABC se, e somente se,
CX (CX é vetor) = CA (CA é vetor) +
 CB (CB é vetor), com
CB (CB é vetor), com  maior (eu não encontrei o símbolo ''maior'') 0 ,
maior (eu não encontrei o símbolo ''maior'') 0 ,  maior que 0, e
maior que 0, e  + beta menor que 1.
+ beta menor que 1. Bom, eu sei que, para que dois vetores sejam paralelos ele tem de ser da forma AB =
 BC,
BC,  real. Mas não consigo usar essa informação para provar... Minha maior dificuldade é sempre em provar e demonstrar... Agradeço imensamente a quem puder dar uma luz. Grato !
real. Mas não consigo usar essa informação para provar... Minha maior dificuldade é sempre em provar e demonstrar... Agradeço imensamente a quem puder dar uma luz. Grato !

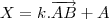
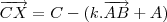
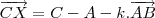
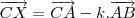
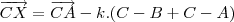
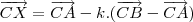
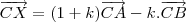
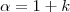

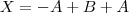

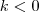
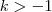

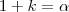
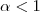

 .
.



