 por PeterHiggs » Sex Set 28, 2012 12:33
por PeterHiggs » Sex Set 28, 2012 12:33
Resolver a equação:
![\sqrt[3]{x+1}-\sqrt[3]{x-1} = \sqrt[6]{x^2-1} \sqrt[3]{x+1}-\sqrt[3]{x-1} = \sqrt[6]{x^2-1}](/latexrender/pictures/169685f382e28eeaeb38c8efd6a7778a.png) Resposta:
Resposta: S =
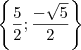
Sei que é uma questão simples, mas, ao tentar resolver, acabei não conseguindo mesmo chegar a um resultado. Sobravam sempre as raízes cúbicas, não consegui sair desse impasse. Alguém pode me ajudar nessa simples e interessante questão de equações irracionais ?
-
PeterHiggs
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Mai 25, 2012 18:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Sex Set 28, 2012 16:19
por young_jedi » Sex Set 28, 2012 16:19
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por PeterHiggs » Sex Set 28, 2012 22:14
por PeterHiggs » Sex Set 28, 2012 22:14
Obrigado young_jedi !
Não era tão simples, não, hehe... !
-
PeterHiggs
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Mai 25, 2012 18:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação Irracional
por luanxd » Ter Fev 09, 2010 23:44
- 2 Respostas
- 2082 Exibições
- Última mensagem por MarceloFantini

Qua Fev 10, 2010 12:38
Sistemas de Equações
-
- equação irracional
por Rosana Vieira » Ter Nov 29, 2011 13:51
- 1 Respostas
- 1608 Exibições
- Última mensagem por ivanfx

Ter Nov 29, 2011 15:04
Funções
-
- Equação irracional
por Flordelis25 » Sáb Abr 20, 2013 17:39
- 2 Respostas
- 1581 Exibições
- Última mensagem por Flordelis25

Sex Mai 24, 2013 17:17
Equações
-
- Equaçao Irracional
por Amanda91 » Qua Jul 10, 2013 03:05
- 3 Respostas
- 1832 Exibições
- Última mensagem por DanielFerreira

Sáb Nov 02, 2013 09:14
Equações
-
- [Equação irracional]
por Victor985 » Qui Dez 12, 2013 20:37
- 1 Respostas
- 1130 Exibições
- Última mensagem por DanielFerreira

Ter Fev 11, 2014 13:38
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{x+1}-\sqrt[3]{x-1} = \sqrt[6]{x^2-1} \sqrt[3]{x+1}-\sqrt[3]{x-1} = \sqrt[6]{x^2-1}](/latexrender/pictures/169685f382e28eeaeb38c8efd6a7778a.png)
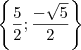


![\sqrt[3]{x+1}-\sqrt[3]{x-1}=\sqrt[6]{x+1}.\sqrt[6]{x-1} \sqrt[3]{x+1}-\sqrt[3]{x-1}=\sqrt[6]{x+1}.\sqrt[6]{x-1}](/latexrender/pictures/4edaad4bb70dc932bb2d3c3a134b2d6a.png)
![\sqrt[6]{x+1}.\sqrt[6]{x+1}-\sqrt[6]{x-1}.\sqrt[6]{x-1}=\sqrt[6]{x+1}.\sqrt[6]{x-1} \sqrt[6]{x+1}.\sqrt[6]{x+1}-\sqrt[6]{x-1}.\sqrt[6]{x-1}=\sqrt[6]{x+1}.\sqrt[6]{x-1}](/latexrender/pictures/5ba61d8b2b21ae5d4110a6b7de19a677.png)
![\frac{\sqrt[6]{x+1}.\sqrt[6]{x+1}}{\sqrt[6]{x+1}.\sqrt[6]{x-1}}-\frac{\sqrt[6]{x-1}.\sqrt[6]{x-1}}{\sqrt[6]{x+1}.\sqrt[6]{x-1}}=1 \frac{\sqrt[6]{x+1}.\sqrt[6]{x+1}}{\sqrt[6]{x+1}.\sqrt[6]{x-1}}-\frac{\sqrt[6]{x-1}.\sqrt[6]{x-1}}{\sqrt[6]{x+1}.\sqrt[6]{x-1}}=1](/latexrender/pictures/29940cbf7549124b5faaf90022a3df36.png)
![\sqrt[6]{\frac{x+1}{x-1}}-\sqrt[6]{\frac{x-1}{x+1}}=1 \sqrt[6]{\frac{x+1}{x-1}}-\sqrt[6]{\frac{x-1}{x+1}}=1](/latexrender/pictures/7112e39994a48a1f617c926efc3493aa.png)
![y=\sqrt[6]{\frac{x+1}{x-1}} y=\sqrt[6]{\frac{x+1}{x-1}}](/latexrender/pictures/739f7edabc783e0d0fa43e42060ba8d2.png)


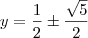
![\sqrt[6]{\frac{x+1}{x-1}}=\frac{1}{2}\pm\frac{\sqrt{5}}{2} \sqrt[6]{\frac{x+1}{x-1}}=\frac{1}{2}\pm\frac{\sqrt{5}}{2}](/latexrender/pictures/a60706515ed185ae36b8540500fa44ef.png)
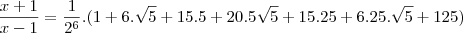



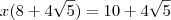




 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
