Gente, Boa noite/tarde/dia.
Estou estudando Derivadas e Integrais que nem um louco, E agora que terminei de estudar, marquei todas as dúvidas para pedir ajuda.Por favor, preciso de voces.
È o seguinte,
Tive uma lista de exercícios que eu fiz, porém as 3 últimas eu nao consegui, e nao entendi a correção do meu Professor.
Ele quer que :
a) Determinar pontos críticos,intervalos de crescimento,decrescimento
b)Valores de máximo e mínimo e pontos de inflexão.
AS ultimas 3 funções :
Da que eu tenho mais desespero para a menos :
h) y = f(x) = sen(x)
g) f(x) = x^4 + 4x^3
f) f(x) = x^3 + 3x^2 + 5x + 3
Entrei no WolfRamalpha e joguei as funções la , mas por exemplo, na H ,
http://www.wolframalpha.com/input/?i=sen%28x%29
Ele me da uma raiz que é um conjunto de numeros, me da uma derivada que nao adianta.
Enfim, nao sei o que fazer...
Nas outras, empaquei em várias partes, e pedi ajuda pra amigos, mas nem eles sabem fazer direito.
Preciso de ajuda.
Comprei um Curso na internet, estou estudando bastante, mas ainda tenho dúvidas.
Voces podem me ajudar?
*Detalhe, esses exercicios ja foram entregues, mas estou estudando eles para a prova.


 então
então  . Os pontos de máximo e mínimo serão atingidos onde a derivada se anular, ou seja,
. Os pontos de máximo e mínimo serão atingidos onde a derivada se anular, ou seja, 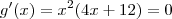 . Continue.
. Continue.


 .
.



