 por babiiimbaa » Qua Set 26, 2012 13:30
por babiiimbaa » Qua Set 26, 2012 13:30
Bom gente, fiz a integral por partes de
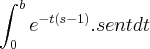
duas vezes e quando substitui o b , apareceu
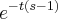
em todos os termos, o que vale 0 quando b tende a infinito. Onde eu estou errando?
-
babiiimbaa
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Ago 29, 2010 19:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por babiiimbaa » Qua Set 26, 2012 13:36
por babiiimbaa » Qua Set 26, 2012 13:36
Acho que descobri onde eu estava errando em contas... deu
1/ ![[({s-1}^{2}) + 1] [({s-1}^{2}) + 1]](/latexrender/pictures/784b3589a060680093708e6980dfbbaf.png)
. Seria isso?
-
babiiimbaa
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Ago 29, 2010 19:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por young_jedi » Qua Set 26, 2012 13:59
por young_jedi » Qua Set 26, 2012 13:59
é
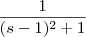
só uma coisa voce poderia resolver utilizando a tabela de transformadas e as propriedades, sem fazer a integral,
mais talvez o objeto do exercicio fosse fazer a integral, não sei.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
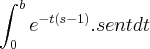 duas vezes e quando substitui o b , apareceu
duas vezes e quando substitui o b , apareceu 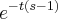 em todos os termos, o que vale 0 quando b tende a infinito. Onde eu estou errando?
em todos os termos, o que vale 0 quando b tende a infinito. Onde eu estou errando?
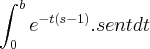 duas vezes e quando substitui o b , apareceu
duas vezes e quando substitui o b , apareceu 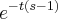 em todos os termos, o que vale 0 quando b tende a infinito. Onde eu estou errando?
em todos os termos, o que vale 0 quando b tende a infinito. Onde eu estou errando?
![[({s-1}^{2}) + 1] [({s-1}^{2}) + 1]](/latexrender/pictures/784b3589a060680093708e6980dfbbaf.png) . Seria isso?
. Seria isso?
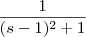


 .
.
 :
: