FAP0151
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por spektroos » Seg Set 24, 2012 01:44
por spektroos » Seg Set 24, 2012 01:44
Me desculpem, sei que esse nao é o lugar certo, porem nao achei outro lugar para poder tirar minha duvida referente a uma questao de tal materia, se algum puder me ajudar ficaria agradecido.
Um corpo é lancado ao nivel do solo com velocidade inicial Vo, esta velocidade faz um angulo ? com relacao a horizontal. Caso fosse possivel acelerar esse objeto na horizontal com uma taxa de 1m/s quadrado. Como seria escrita as relacoes de Hmax e Xmax para este movimento?
-
spektroos
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Seg Set 24, 2012 01:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Civil
- Andamento: cursando
 por MarceloFantini » Seg Set 24, 2012 03:06
por MarceloFantini » Seg Set 24, 2012 03:06
A equação para a altura máxima não muda, mas o comprimento horizontal máximo com certeza aumenta. Com uma aceleração constante a velocidade aumenta linearmente, altere as equações para este fato.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por spektroos » Seg Set 24, 2012 19:37
por spektroos » Seg Set 24, 2012 19:37
-
spektroos
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Seg Set 24, 2012 01:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Civil
- Andamento: cursando
 por spektroos » Seg Set 24, 2012 20:09
por spektroos » Seg Set 24, 2012 20:09
Em relacao a questao de fisica, isso aqui nao tem nada a ver né?

-
spektroos
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Seg Set 24, 2012 01:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Civil
- Andamento: cursando
 por young_jedi » Seg Set 24, 2012 20:19
por young_jedi » Seg Set 24, 2012 20:19
O Hmax esta correto, por Torriceli voce chega nisto
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por spektroos » Seg Set 24, 2012 20:35
por spektroos » Seg Set 24, 2012 20:35
Entao o xmax esta errado? O que seria esse torriceli? que acredito nao ter visto isso ainda.
-
spektroos
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Seg Set 24, 2012 01:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Civil
- Andamento: cursando
 por young_jedi » Seg Set 24, 2012 20:48
por young_jedi » Seg Set 24, 2012 20:48
a equação de Torriceli(não tenho certeza se é assim que se escreve)
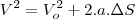
onde V é a velocidade final e Vo é a velocidade inicial, a é a aceleração e
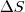
é o deslocamento
nesse caso a altura maxima é quando a velocidade chega a 0, substitutindo os valore chega na equação que voce colocou
O Xmax eu não sei se esta certo, não sei como voce chegou nessa relação, mais da pra voce encontrar ele da maneira que eu coloquei no seu outro post
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Fundamentos de Mecânica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ajuda com projeto de física
por daniloadanilo » Dom Set 05, 2010 23:32
- 1 Respostas
- 3251 Exibições
- Última mensagem por Neperiano

Seg Jul 18, 2011 23:09
Desafios Fáceis
-
- Cáuculo de Física [AJUDA URGENTE!]
por MateusJunior » Qui Mar 03, 2011 18:41
- 2 Respostas
- 2060 Exibições
- Última mensagem por MateusJunior

Sex Mar 04, 2011 14:23
Álgebra Elementar
-
- [física] Ajuda Pelo amor d Deus
 por thialarcon1 » Sex Jun 13, 2008 13:59
por thialarcon1 » Sex Jun 13, 2008 13:59
- 4 Respostas
- 5223 Exibições
- Última mensagem por Neperiano

Seg Jun 18, 2012 18:11
Dúvidas Pendentes (aguardando novos colaboradores)
-
- (pêndulo-física)alguém ajuda achar energia potencial ?
por gustavoluiss » Ter Set 06, 2011 15:17
- 6 Respostas
- 3961 Exibições
- Última mensagem por gustavoluiss

Qua Set 07, 2011 01:55
Álgebra Elementar
-
- Física
por Mi_chelle » Qua Abr 13, 2011 17:52
- 3 Respostas
- 5011 Exibições
- Última mensagem por Mi_chelle

Qui Abr 14, 2011 00:07
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.









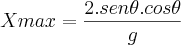



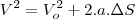
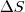 é o deslocamento
é o deslocamento

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.