


 onde
onde  . Progressões aritméticas e geométricas são apenas sequências com regras bem simples.
. Progressões aritméticas e geométricas são apenas sequências com regras bem simples.

MarceloFantini escreveu:Polinômios e interpolação de Lagrange são relacionadas entre si, mas qual a relação com progressões aritméticas?[...]
MarceloFantini escreveu:Também não sei o que quer dizer com P.A. de segunda ou primeira ordem. A primeira sequência que passou não é uma progressão aritmética, mas a segunda é. A terceira pode ser encarada como uma P.A. com razão igual a zero.

Ora, um polinômio de grau um é uma reta no plano XY e ele pode ser descrito como uma PA. Um polinômio de grau dois é uma parábola no plano XY e parábola é resultado duma PA de 2ª ordem (ou duma integral de segunda ordem (não sei se integral tem ordens))
Sério? Eu não sei se estou descrevendo tudo usando os termos matemáticos corretos ou incorretos (certas vezes escrevo algo que suspeito estar errado para ver se serei corrijido ou não e aprender com isso...), mas PA de 2ª ordem é abordado nas video aulas do IMPA, no youtube... :|


MarceloFantini escreveu:Progressões são, por definição, discretas[...]
MarceloFantini escreveu:Sério? Eu não sei se estou descrevendo tudo usando os termos matemáticos corretos ou incorretos (certas vezes escrevo algo que suspeito estar errado para ver se serei corrijido ou não e aprender com isso...), mas PA de 2ª ordem é abordado nas video aulas do IMPA, no youtube... :|
Poderia providenciar um link? Assim facilitaria a discussão.






MarceloFantini escreveu:Assisti a porção do vídeo que você disse [...]

Enta tá... vamos por partes... Uma função polinomial é diferente duma função exponencial e de potêncial ou de qualquer outra gênero, certo? Entendo assim porque dado dois pontos no plano XY do GeoGebra, a equação da regressão bivariada polinomial, exponencial e de potência que ele calcula, são diferentes entre si. Portanto, deve existir diferentes fórmulas para determinar essas diferentes equações, e a interpolação de Lagrange é uma delas, certo?


MarceloFantini escreveu:Enta tá... vamos por partes... Uma função polinomial é diferente duma função exponencial e de potêncial ou de qualquer outra gênero, certo? Entendo assim porque dado dois pontos no plano XY do GeoGebra, a equação da regressão bivariada polinomial, exponencial e de potência que ele calcula, são diferentes entre si. Portanto, deve existir diferentes fórmulas para determinar essas diferentes equações, e a interpolação de Lagrange é uma delas, certo?
Certo. Não sei o que é essa regressão bivariada polinomial, mas os polinômios de Lagrange são os polinômios de menor grau em que as funções coincidem em cada ponto especificado.




 . Agora façamos a distributiva:
. Agora façamos a distributiva:  .
.  é uma função de
é uma função de  , enquanto que
, enquanto que  é um coeficiente angular e
é um coeficiente angular e  é um coeficiente linear. Então a reta que coincide nos inteiros com a P.A. tem coeficiente angular
é um coeficiente linear. Então a reta que coincide nos inteiros com a P.A. tem coeficiente angular  e coeficiente linear
e coeficiente linear  .
.  e termo inicial
e termo inicial  , então teremos uma reta passando por
, então teremos uma reta passando por  , crescente e que cada variação de
, crescente e que cada variação de  será metade da variação
será metade da variação  .
.


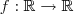 por
por
 coincide com a sequência mas vale qualquer outra coisa nos outros pontos.
coincide com a sequência mas vale qualquer outra coisa nos outros pontos.

MarceloFantini escreveu:Você quer dizer P.A. ou P.G.?
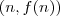 duma P.G. :S
duma P.G. :S






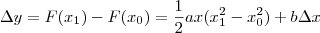

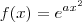 , por ex., é uma função exponencial ou de potencia?
, por ex., é uma função exponencial ou de potencia?


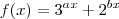 ,por exemplo, elas não são exploradas e estudadas?
,por exemplo, elas não são exploradas e estudadas?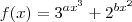
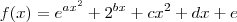

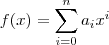 , enquanto que uma exponencial é
, enquanto que uma exponencial é 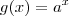 , com
, com  e
e 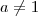 .
.

 mas o wolframalpha sim e detalhe, este plota tal função tanto no Plano Real quanto no Imaginário!
mas o wolframalpha sim e detalhe, este plota tal função tanto no Plano Real quanto no Imaginário!
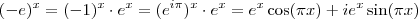 .
.


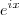 ? Ela responde tudo. Ela é um número complexo da forma
? Ela responde tudo. Ela é um número complexo da forma 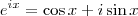 . Logo, quando você plota a parte real e parte imaginárias separadamente você tem um cosseno e seno, respectivamente. No caso de
. Logo, quando você plota a parte real e parte imaginárias separadamente você tem um cosseno e seno, respectivamente. No caso de 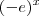 você tem uma exponencial multiplicando, o que altera a amplitude do gráfico em cada ponto.
você tem uma exponencial multiplicando, o que altera a amplitude do gráfico em cada ponto.

MarceloFantini escreveu:Você conhece a função exponencial complexa? Ela responde tudo. Ela é um número complexo da forma
. Logo, quando você plota a parte real e parte imaginárias separadamente você tem um cosseno e seno, respectivamente. No caso de
você tem uma exponencial multiplicando, o que altera a amplitude do gráfico em cada ponto.
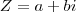 tem coordenadas
tem coordenadas  . Quando define-se que
. Quando define-se que 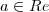 e que
e que 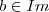 isso ainda não torna as coisas claras para mim, porque surgem mais 5 novas perspectivas numéricas:
isso ainda não torna as coisas claras para mim, porque surgem mais 5 novas perspectivas numéricas:  e
e  , que não sei interpretá-las muito bem. Portanto, pergunto: alguns desses 5 termos mantém alguma relação de identidade com
, que não sei interpretá-las muito bem. Portanto, pergunto: alguns desses 5 termos mantém alguma relação de identidade com  ou com
ou com  , sendo que esta relação de identidade pode ser apenas numericamente igual? Ou seja, gostaria de saber se há alguma relação biunívoca entre qualquer um dos 5 valores que eu citei com x ou com y.
, sendo que esta relação de identidade pode ser apenas numericamente igual? Ou seja, gostaria de saber se há alguma relação biunívoca entre qualquer um dos 5 valores que eu citei com x ou com y.
Um número complexotem coordenadas
. Quando define-se que
e que
isso ainda não torna as coisas claras para mim, porque surgem mais 5 novas perspectivas numéricas:
e
, que não sei interpretá-las muito bem. Portanto, pergunto: alguns desses 5 termos mantém alguma relação de identidade com
ou com
, sendo que esta relação de identidade pode ser apenas numericamente igual? Ou seja, gostaria de saber se há alguma relação biunívoca entre qualquer um dos 5 valores que eu citei com x ou com y.
 , então temos que
, então temos que  e
e  são números reais, ou seja,
são números reais, ou seja, 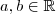 . Nós os distinguimos dizendo que
. Nós os distinguimos dizendo que  é a parte real do número complexo e
é a parte real do número complexo e  é a parte imaginária, em notação:
é a parte imaginária, em notação:  e
e  .
.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)