como eu faço pra esboçar o ponto (0,0,0) no plano tridimensional?
(Eu achava q era a origem do plano, mas meu prof disse que não é)

Se tiver como, coloquem uma imagem, por favor, pra ficar mais fácil a visualização,
Obrigada. att.
Samara






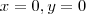 e
e  representam planos em
representam planos em  , que são o plano
, que são o plano 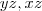 e
e  respectivamente. A interseção desses três planos é a origem. Tente fazer o desenho pensando nisso agora.
respectivamente. A interseção desses três planos é a origem. Tente fazer o desenho pensando nisso agora.


Voltar para Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

