 por Babi1234 » Sex Set 14, 2012 17:46
por Babi1234 » Sex Set 14, 2012 17:46
Um capital aumentado de seus juros simples durante 18 meses se elevou a $437.575,00. Esse mesmo capital diminuido de seus juros simples durante 405 dias ficou reduzido a $337.693,75. Determinar a texa anual empregada. R:10%a.a
Nao consigo chegar a essa resposta de forma alguma. Se alguem conseguir dedsenvolver esse problema eu ia agradecer mmmuuuiitoo!!

-
Babi1234
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sex Set 14, 2012 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por Cleyson007 » Sex Set 14, 2012 18:18
por Cleyson007 » Sex Set 14, 2012 18:18
Boa tarde Babi!
Seja bem-vinda ao AjudaMatemática!
Bom, eu também não encontrei a resposta do seu gabarito.. Estou fazendo assim:
C + J1 = X1 --> (Montante)
C.(1+ 1,5.i) = $437.575,00 (I)
C - J2 = X2
C - C . i . (405/360) = $337.693,75
C . (1 - 1,125.i) = 4337.693,75 (II)
Dividindo (I) por (II), temos:
(1 + 1,5.i)/(1 - 1,125.i) = 1,2957
Resolvendo, i = 1% a.a.
Vamos ver o que os demais amigos do fórum diz.
Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Babi1234 » Sex Set 14, 2012 18:28
por Babi1234 » Sex Set 14, 2012 18:28
Obrigado!! To achando que o gabarito esta errado. Encontrei essa questao em outro lugar e a resporta encontrada tbm foi 1%aa.
-
Babi1234
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sex Set 14, 2012 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por DanielFerreira » Sáb Set 15, 2012 10:40
por DanielFerreira » Sáb Set 15, 2012 10:40
Babi1234 escreveu:Um capital aumentado de seus juros simples durante 18 meses se elevou a $437.575,00.
Capital (P) = ?
Juros (J) = ?
Montante (S) = R$ 437.575,00
Prazo (n) = 18m
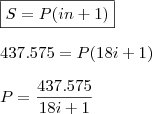
Babi1234 escreveu:Esse mesmo capital diminuido de seus juros simples durante 405 dias ficou reduzido a $337.693,75.
Passando o prazo de dias para meses, temos:
405 dias = 13,5 meses
Então,
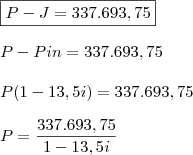
Babi1234 escreveu:Determinar a texa anual empregada. R:10%a.a
Basta igualar

e converter a taxa para anual, pois a taxa que iremos encontrar é mensal (estávamos calculando em meses).
Segue,
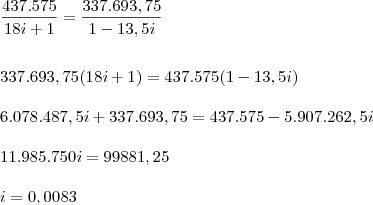
Ou seja, a taxa é
0,83% a.m Como foi dito anteriormente, devemos convertê-la.
0,83% a.m =
0,83%

12 =
10% a.a"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por ana celia » Dom Out 21, 2012 21:56
por ana celia » Dom Out 21, 2012 21:56
Olá amigos , não consegui nem sair do exercícios
obrigada.
Em um mesmo dia, 1/3 de certo capital foi aplicado por 8 meses a uma taxa de juros simples de 18% ao ano, e o restante foi aplicado também por 8 meses, mas uma taxa de juros simples de 21% ao ano.No final, obteve-se um total de R$ 6.800,00 de juros pelas duas aplicações.O valor total aplicado foi de
resposta 51.000,00
-
ana celia
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Set 11, 2012 10:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por Babi1234 » Dom Out 21, 2012 23:07
por Babi1234 » Dom Out 21, 2012 23:07
PV1= PV/3
i1= 1,5%a.m (8%/12)
N1=8 meses
FV1=?
PV2= 2PV/3
i2= 1,75% a.m
N2=8 meses
FV2=?
FV1 + FV2 = 6800 + PV
Substituindo o fv1 e fv2 na expressao a cima pela formula de juros simple, temos:
PV/3 (1+0,015x8) + 2PV/3 (1+0,0175x8) = 6800 + PV
1,12PV + 2,28PV = 20400 + 3PV
0,40PV = 20400
PV = 51000
-
Babi1234
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sex Set 14, 2012 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por Babi1234 » Dom Out 21, 2012 23:17
por Babi1234 » Dom Out 21, 2012 23:17
ana celia escreveu:Olá amigos , não consegui nem sair do exercícios
obrigada.
Em um mesmo dia, 1/3 de certo capital foi aplicado por 8 meses a uma taxa de juros simples de 18% ao ano, e o restante foi aplicado também por 8 meses, mas uma taxa de juros simples de 21% ao ano.No final, obteve-se um total de R$ 6.800,00 de juros pelas duas aplicações.O valor total aplicado foi de
resposta 51.000,00
PV1= PV/3
i1= 1,5%a.m (8%/12)
N1=8 meses
FV1=?
PV2= 2PV/3
i2= 1,75% a.m
N2=8 meses
FV2=?
FV1 + FV2 = 6800 + PV
Substituindo o fv1 e fv2 na expressao a cima pela formula de juros simple, temos:
PV/3 (1+0,015x8) + 2PV/3 (1+0,0175x8) = 6800 + PV
1,12PV + 2,28PV = 20400 + 3PV
0,40PV = 20400
PV = 51000
-
Babi1234
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sex Set 14, 2012 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por DanielFerreira » Seg Out 22, 2012 18:34
por DanielFerreira » Seg Out 22, 2012 18:34
ana celia escreveu:Olá amigos , não consegui nem sair do exercícios
obrigada.
Em um mesmo dia, 1/3 de certo capital foi aplicado por 8 meses a uma taxa de juros simples de 18% ao ano, e o restante foi aplicado também por 8 meses, mas uma taxa de juros simples de 21% ao ano.No final, obteve-se um total de R$ 6.800,00 de juros pelas duas aplicações.O valor total aplicado foi de
resposta 51.000,00
Ana Celia,
procure abrir um
tópico para sua dúvida. Vamos manter o Fórum organizado.
Att,
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Juros Simples // Juros Compostos
por Roberta » Qui Jul 16, 2009 18:22
- 3 Respostas
- 8213 Exibições
- Última mensagem por Roberta

Qui Jul 16, 2009 19:46
Matemática Financeira
-
- Juros Simples
por Gir » Ter Set 01, 2009 11:03
- 1 Respostas
- 8306 Exibições
- Última mensagem por Lucio Carvalho

Ter Set 01, 2009 17:24
Matemática Financeira
-
- juros simples
por sandi » Seg Out 05, 2009 23:58
- 1 Respostas
- 3749 Exibições
- Última mensagem por DanielFerreira

Seg Mar 29, 2010 11:49
Matemática Financeira
-
- Juros Simples
por Livia Primo » Seg Mar 15, 2010 19:13
- 1 Respostas
- 4746 Exibições
- Última mensagem por DanielFerreira

Seg Mar 15, 2010 19:20
Pedidos
-
- JUROS SIMPLES
por Liliani » Seg Abr 05, 2010 17:47
- 5 Respostas
- 6472 Exibições
- Última mensagem por aldhemah

Qua Abr 07, 2010 00:19
Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






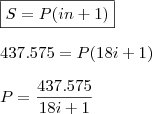
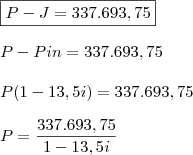
 e converter a taxa para anual, pois a taxa que iremos encontrar é mensal (estávamos calculando em meses).
e converter a taxa para anual, pois a taxa que iremos encontrar é mensal (estávamos calculando em meses).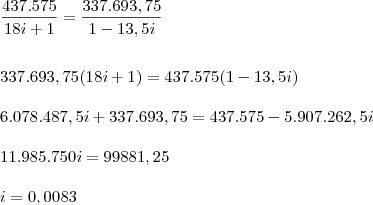
 12 =
12 =






 , avisa que eu resolvo.
, avisa que eu resolvo.

