Fundamentos da Matemática Elementar, vol 6, exercício 16, pag 11:
Quais os números complexos x e y para os quais : x + yi = i e xi + y = 2i - 1 .
Seguindo o raciocínio que eu aprendi a ter até agora pelas coisas ditas pelo livro eu consideraria isso daí duas funções separadas e diria que para a primeira, considerando que real é igual a real e imaginário é igual a imaginário, diria que:
x = 0 e y = 1 ; na segunda eu diria que : x = 2 e y = -1 entretanto o gabarito é único e me apresenta a seguinte resposta:
x = 1 + i ; y = i
Logo em seguida vem o exercício 18, na pag 12:
Qual a condição para que o número
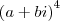 , a e b reais, seja estritamente negativo?
, a e b reais, seja estritamente negativo?Nesse aí eu parti do seguinte princípio:
 , então eu cheguei a algo como
, então eu cheguei a algo como ![{(a+bi)}^{4} = {[(a+bi)}^{2}]^{2} = {({a}^{2}-{b}^{2}+2abi)}^{2} {(a+bi)}^{4} = {[(a+bi)}^{2}]^{2} = {({a}^{2}-{b}^{2}+2abi)}^{2}](/latexrender/pictures/dfdefc57b1a35b851ae34a31f5224b3e.png) ; então:
; então:  , sendo essa última menor que zero, pois a condição do enunciado é que sejam menores que zero, então:
, sendo essa última menor que zero, pois a condição do enunciado é que sejam menores que zero, então:  ; disso eu consigo dizer somente que ab tem que ser diferentes de zero;
; disso eu consigo dizer somente que ab tem que ser diferentes de zero; já na resposta do livro o gabarito também chega a conclusão de que a = +-b ; essa última parte eu não sei como ele alcançou ou se minhas ponderações até aqui também foram corretas.
Obrigado a quem ler e se interessar a responder. Att, Rafael.


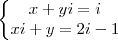
 e
e  , de 2 equações. Portanto o par
, de 2 equações. Portanto o par 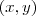 da 1° equação é identico ao par
da 1° equação é identico ao par  .
.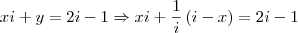 ,
, .
. .
.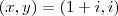 .
.
 . Portanto, a solução
. Portanto, a solução  é correta porém, de certa forma, inadequada. Para resolver este problema basta que você multiplique o denominador e numerador pelo conjugado do número complexo que aparece no denominador.
é correta porém, de certa forma, inadequada. Para resolver este problema basta que você multiplique o denominador e numerador pelo conjugado do número complexo que aparece no denominador. .
. é
é  . Portanto, segue o processo. Apenas uma observação: esta regra não é a da racionalização, visto que nesta o interesse é em escrever o denominador como um número racional( daí, racionalizar). Nosso objetivo é tornar o denominador real.
. Portanto, segue o processo. Apenas uma observação: esta regra não é a da racionalização, visto que nesta o interesse é em escrever o denominador como um número racional( daí, racionalizar). Nosso objetivo é tornar o denominador real.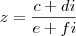
 , visto que o produto de um numero complexo por seu conjugado é sempre um número real puro!
, visto que o produto de um numero complexo por seu conjugado é sempre um número real puro!

 .
.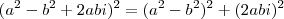
 com
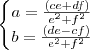
com  para que o complexo apresentado seja um real puro! Para tanto é necessário que sua parte imaginária seja nula. Vamos expandir o complexo para isolar sua parte real e imaginária:
para que o complexo apresentado seja um real puro! Para tanto é necessário que sua parte imaginária seja nula. Vamos expandir o complexo para isolar sua parte real e imaginária:![(a+bi)^{4}=[(a+bi)^{2}]^{2} = (a^{2}-b^{2}+2abi)^{2} = (a^{2}-b^{2}+2abi)(a^{2}-b^{2}+2abi) (a+bi)^{4}=[(a+bi)^{2}]^{2} = (a^{2}-b^{2}+2abi)^{2} = (a^{2}-b^{2}+2abi)(a^{2}-b^{2}+2abi)](/latexrender/pictures/c08937a213c7515a2376dfb8a85ff409.png)

 .
.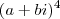 é
é  que deve ser nula. Portanto,
que deve ser nula. Portanto, .
.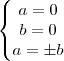
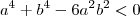
 , então
, então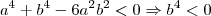 ,
, acontecerá o mesmo!
acontecerá o mesmo! , temos
, temos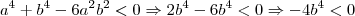 .
. .
.![\sqrt[3]{-11-2i} \sqrt[3]{-11-2i}](/latexrender/pictures/dd0627ec5e478d7b61a8f7c4a7c05ce9.png)
![\sqrt[4]{28-96i} \sqrt[4]{28-96i}](/latexrender/pictures/5cf4fdfd1c7fa2b54dd0ce17967ccdc0.png)
![\frac{-1+2\sqrt[2]{3}}{2}+\frac{\sqrt[2]{3}-2} { 2 } i \frac{-1+2\sqrt[2]{3}}{2}+\frac{\sqrt[2]{3}-2} { 2 } i](/latexrender/pictures/24a072a19043a10ec7c3ea59e63c2d03.png) ou
ou ![\frac{-1-2\sqrt[2]{3}}{2}-\frac{\sqrt[2]{3}-2} { 2 } i \frac{-1-2\sqrt[2]{3}}{2}-\frac{\sqrt[2]{3}-2} { 2 } i](/latexrender/pictures/078ff3bde8a90ebdae5d5e838be5db33.png)
 raízes
raízes  um complexo de argumento
um complexo de argumento  . Assim,
. Assim,
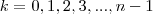 .
.![\sqrt[3]{-11-2i} = (\sqrt[]{11^2+2^2})^\frac{1}{3}\left(cos(n\theta+2nk\pi)+i.sin(n\theta+2nk\pi) \right) \sqrt[3]{-11-2i} = (\sqrt[]{11^2+2^2})^\frac{1}{3}\left(cos(n\theta+2nk\pi)+i.sin(n\theta+2nk\pi) \right)](/latexrender/pictures/93e38e6ef757d2d70369fd696547c5fa.png)
 .
.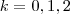 e calcule as 3 raízes.
e calcule as 3 raízes.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)