 por jaegger » Qui Set 06, 2012 10:06
por jaegger » Qui Set 06, 2012 10:06
Olá todo mundo, de alguns exercicios de trigo, tenho 2 que não consigo resolver, sera que alguém me consegue ajudar?
1º Resolver a equação :

2ºResolver a equação :
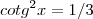
Depois tenho que representar no circulo trigonométrico.
Obrigado pessoal.
-
jaegger
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Set 06, 2012 09:47
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: cursando
 por LuizAquino » Qui Set 06, 2012 12:47
por LuizAquino » Qui Set 06, 2012 12:47
jaegger escreveu:Olá todo mundo, de alguns exercicios de trigo, tenho 2 que não consigo resolver, sera que alguém me consegue ajudar?
1º Resolver a equação :

2ºResolver a equação :
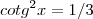
Depois tenho que representar no circulo trigonométrico.
Você disse que de alguns exercícios estes são os que você não conseguiu fazer. Mas você chegou a tentar alguma coisa neles? Até onde você conseguiu desenvolver?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jaegger » Qui Set 06, 2012 17:38
por jaegger » Qui Set 06, 2012 17:38
Bem, para o 1º tentei :
![cos^2(x+2pi/3)-sin^2(x+2pi/3)=0
[cos(x+2pi/3)-sin(x+2pi/3)][cos(x+2pi/3)+sin(x+2pi/3)]=0
cos(x+2pi/3)-sin(x+2pi/3)=0 ou cos(x+2pi/3)+sin(x+2pi/3)=0 cos^2(x+2pi/3)-sin^2(x+2pi/3)=0
[cos(x+2pi/3)-sin(x+2pi/3)][cos(x+2pi/3)+sin(x+2pi/3)]=0
cos(x+2pi/3)-sin(x+2pi/3)=0 ou cos(x+2pi/3)+sin(x+2pi/3)=0](/latexrender/pictures/27ece87d5f7aa42b3dc24e242885bf9d.png)
mas depois não lhe sei dar a volta.
Para o segundo sei que
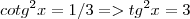
, será que devo pegar com
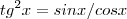
?
Sera que assim vou la´?
-
jaegger
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Set 06, 2012 09:47
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: cursando
 por LuizAquino » Sáb Set 08, 2012 14:51
por LuizAquino » Sáb Set 08, 2012 14:51
jaegger escreveu:Bem, para o 1º tentei :
![cos^2(x+2pi/3)-sin^2(x+2pi/3)=0
[cos(x+2pi/3)-sin(x+2pi/3)][cos(x+2pi/3)+sin(x+2pi/3)]=0
cos(x+2pi/3)-sin(x+2pi/3)=0 ou cos(x+2pi/3)+sin(x+2pi/3)=0 cos^2(x+2pi/3)-sin^2(x+2pi/3)=0
[cos(x+2pi/3)-sin(x+2pi/3)][cos(x+2pi/3)+sin(x+2pi/3)]=0
cos(x+2pi/3)-sin(x+2pi/3)=0 ou cos(x+2pi/3)+sin(x+2pi/3)=0](/latexrender/pictures/27ece87d5f7aa42b3dc24e242885bf9d.png)
mas depois não lhe sei dar a volta.
Para o segundo sei que
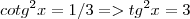
, será que devo pegar com
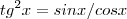
?
Sera que assim vou la´?
A ideia básica na resolução de uma equação trigonométrica é deixá-la em um formato que só apareça um das funções trigonométricas. Ou seja, que só apareça seno, ou só apareça cosseno, ou só tangente, etc.
Na primeira equação, lembrando da identidade fundamental
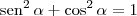
, podemos escrever que:
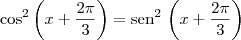
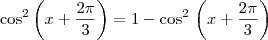
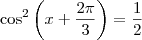
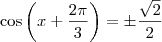
Se considerarmos que estamos trabalhando no intervalo
![[0, 2\pi] [0, 2\pi]](/latexrender/pictures/55a5896fe18d9a8d28b6903719b4e376.png)
, sabemos que
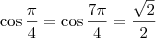
e
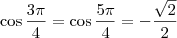
. Temos então quatro possibilidades:
(i)
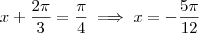
;
(ii)
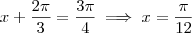
;
(iii)
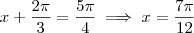
;
(iv)
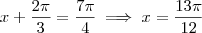
;
Lembrando que o ângulo
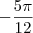
é o mesmo que o ângulo
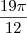
, podemos dizer que a solução (em ordem crescente) da equação é dada por
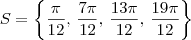
. Agora tente esboçar essa solução no círculo trigonométrico.
Já em relação a segunda equação, tente resolvê-la. Note que você já tem
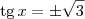
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

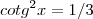


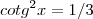


![cos^2(x+2pi/3)-sin^2(x+2pi/3)=0
[cos(x+2pi/3)-sin(x+2pi/3)][cos(x+2pi/3)+sin(x+2pi/3)]=0
cos(x+2pi/3)-sin(x+2pi/3)=0 ou cos(x+2pi/3)+sin(x+2pi/3)=0 cos^2(x+2pi/3)-sin^2(x+2pi/3)=0
[cos(x+2pi/3)-sin(x+2pi/3)][cos(x+2pi/3)+sin(x+2pi/3)]=0
cos(x+2pi/3)-sin(x+2pi/3)=0 ou cos(x+2pi/3)+sin(x+2pi/3)=0](/latexrender/pictures/27ece87d5f7aa42b3dc24e242885bf9d.png)
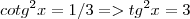 , será que devo pegar com
, será que devo pegar com 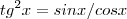 ?
?
, será que devo pegar com
?
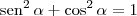 , podemos escrever que:
, podemos escrever que: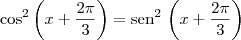
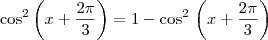
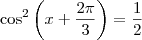
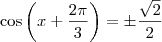
![[0, 2\pi] [0, 2\pi]](/latexrender/pictures/55a5896fe18d9a8d28b6903719b4e376.png) , sabemos que
, sabemos que 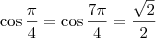 e
e 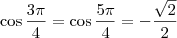 . Temos então quatro possibilidades:
. Temos então quatro possibilidades: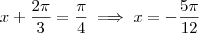 ;
;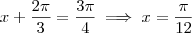 ;
;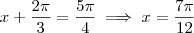 ;
;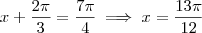 ;
;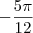 é o mesmo que o ângulo
é o mesmo que o ângulo 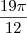 , podemos dizer que a solução (em ordem crescente) da equação é dada por
, podemos dizer que a solução (em ordem crescente) da equação é dada por 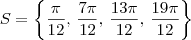 . Agora tente esboçar essa solução no círculo trigonométrico.
. Agora tente esboçar essa solução no círculo trigonométrico.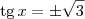 .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
