Não consigo fazer esses exercicios, alguém me ajuda?
Se não são permitidas repetições e utilizando somente os algarismos 0,1,2,3,4,5,6:
a) quantos números de 4 algarismos podemos formar?
b) quantos desses números de 4 algarismos são pares?
b) quantos desses números de 4 algarismos são maiores que 2000?
Com os algarismos 1,2,3,4,5 e 6, quanto s números de 3 algarismos distintos menores que 400 podemos formar?
Um colegiado de 5 membros será selecionado dentre 12 candidatos a membros titulares e 8 candidatos a membros suplentes. De quantas maneiras isso pode ser feito se o colegiado deve consistir
b) de pelo menos 2 titulares e 1 suplente?







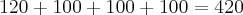 números pares.
números pares. números maiores que 2000.
números maiores que 2000. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.