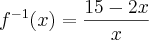
Obtenha a inversa da função abaixo:

- Eu resolvi da forma abaixo:
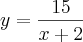
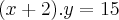
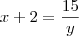

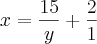
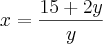
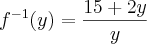
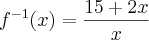
- Não vejo nada de errado, muito pelo contrário, vejo e na forma com meu professor fez, mas ele insiste que a resposta é a função abaixo:
 e portanto,
e portanto, 
- Pelo AMOR DE DEUS(desespero)! Por favor, alguém poderia me explica o porquê desta bruxaria!?

Abraços e obrigado desde já.
Att. Matheus L. Oliveira.


 .
. .
. . Podemos verificar fazendo
. Podemos verificar fazendo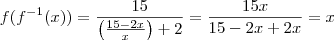



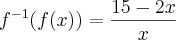


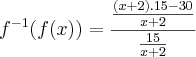
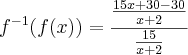

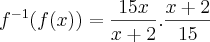

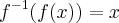
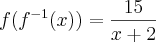


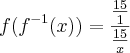



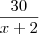 . Em suma, eu pulei algumas passagens.
. Em suma, eu pulei algumas passagens.
 .
.



