Reta e plano

[CarolMarques]

O detonador de uma bomba esta localizado no ponto P = (2; 1; 2). Para provocar a explosão, acende-se a extremidade A = (2; 1; 1) de uma haste combustvel paralela ao vetor u = (1; 0; 2), cuja extremidade B toca o ponto inicial de um rastilho de polvora retilneo que termina no detonador. Sabendo que o fogo se propaga com velocidade unitaria na haste e no rastilho e que este esta contido no plano  : x + 2y z 2 = 0; mostre que a explosão ocorre entre 3 e 4 segundos apos o incio do processo. O
sistema de coordenadas e ortogonal.

Eu não consegui montar o desenho da questão.Só me ajudem nessa parte , de construção do desenho,a partir daí eu tento continuar a questão.

[LuizAquino]

O detonador de uma bomba esta localizado no ponto P = (2; 1; 2). Para provocar a explosão, acende-se a extremidade A = (2; 1; 1) de uma haste combustvel paralela ao vetor u = (1; 0; 2), cuja extremidade B toca o ponto inicial de um rastilho de polvora retilneo que termina no detonador. Sabendo que o fogo se propaga com velocidade unitaria na haste e no rastilho e que este esta contido no plano  : x + 2y z 2 = 0; mostre que a explosão ocorre entre 3 e 4 segundos apos o incio do processo. O
sistema de coordenadas e ortogonal.

Eu não consegui montar o desenho da questão.Só me ajudem nessa parte , de construção do desenho,a partir daí eu tento continuar a questão.

Por favor, revise a equação do plano pois você esqueceu de colocar os sinais para os termos z e 2.

[CarolMarques]

Desculpe,

x+2y-z-2=0

[LuizAquino]

O detonador de uma bomba esta localizado no ponto P = (2; 1; 2). Para provocar a explosão, acende-se a extremidade A = (2; 1; 1) de uma haste combustvel paralela ao vetor u = (1; 0; 2), cuja extremidade B toca o ponto inicial de um rastilho de polvora retilneo que termina no detonador. Sabendo que o fogo se propaga com velocidade unitaria na haste e no rastilho e que este esta contido no plano  : x + 2y z 2 = 0; mostre que a explosão ocorre entre 3 e 4 segundos apos o incio do processo. O
sistema de coordenadas e ortogonal.

Eu não consegui montar o desenho da questão. Só me ajudem nessa parte , de construção do desenho,a partir daí eu tento continuar a questão.

Desculpe,

x + 2y - z - 2 = 0

Assim como você solicitou, segue abaixo um esboço para a situação descrita no exercício.

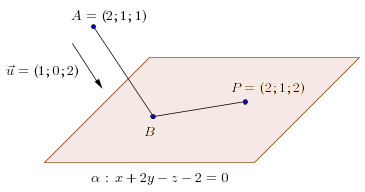
figura.png (4.86 KiB) Exibido 3049 vezes